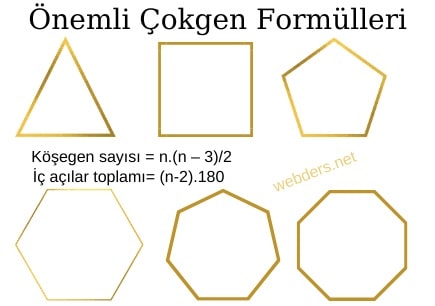
Çokgenler Formülleri
Çokgenler geometrinin en önemli konuları arasında yer almaktadır. Çünkü birbirinden farklı birçok geometrik şekli barındırır. Daha önce çokgenler konu anlatımı kısmında bu konuyu detaylı olarak anlatmıştık. Bu yazıda ise çokgenler konusuyla ilgili formülleri vererek toplu bir şekilde formülleri bulmanızı sağlayacağız. 7. sınıf müfredatından itibaren bu formüller işimize çok yarayacaktır. Çokgenler konveks ...
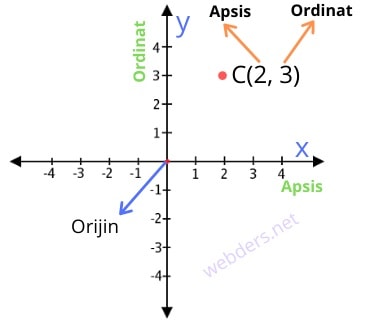
Okumaya devam etOrdinat Nedir?
Analitik geometride bütün noktaları koordinat düzlemi üzerinde göstermekteyiz. Ayrıca matematikte denklem grafiklerini de aynı şekilde koordinat düzlemi üzerinde görürüz. Bir noktanın koordinat düzlemi üzerindeki yerine o noktanın koordinatı denir. İki boyutlu koordinat düzlemi apsis ve ordinat değerlerinden oluşur. Bu yazıda ordinat nedir sorusunu cevaplayacak ve bu bağlamda bilgiler vereceğiz. Koordinat düzleminde ...
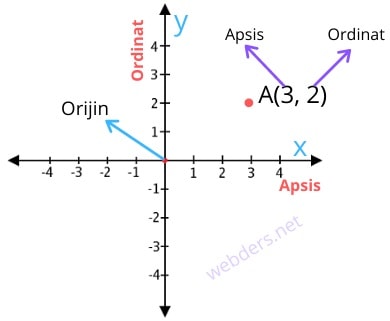
Okumaya devam etApsis Nedir?
Matematikte bir noktanın yerini belli eden düzleme koordinat düzlemi denir. İki boyutlu koordinat düzlemi üzerinden nokta, doğru ya da doğru parçalarının geometrik yerini ifade edebiliriz. Koordinat sistemindeki kavramlardan biri de apsis kavramıdır. Bu yazıda apsis nedir öğrenmeye çalışacağız. Koordinat düzlemindeki yatay eksene apsis ekseni, bu eksen üzerindeki değerlerin her birine ise ...
Okumaya devam etDairenin Alan Formülü
Bir merkez noktasına eşit uzaklıklara sahip noktalar kümesine çember denir. Çemberin içini tararsak da daire elde ederiz. Dolayısıyla çemberin çevresi varken dairenin aynı zamanda alanı da vardır. Bu yazıda dairenin alan formülü üzerinde duracak ve bazı örneklerle öğrendiğimizi pekiştireceğiz. Dairenin alan formülü A = π.r2 şeklindedir. Burada π sabit bir sayıdır ...
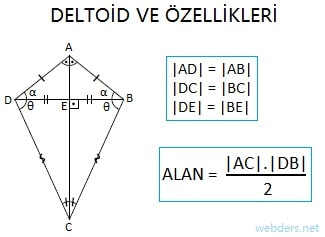
Okumaya devam etDeltoid Özellikleri
Geometride rastladığımız şekillerinden ilginç bir tanesi de deltoid dediğimiz geometrik şekildir. Karşımıza çıkacak herhangi bir deltoid sorusunu çözebilme için deltoidin özelliklerini iyi bilmemiz gerekiyor. Öyleyse önce deltoid nedir diyerek konuya başlayalım. Ortak tabana sahip iki ikizkenar üçgenin bir araya gelmesiyle oluşan dörtgene deltoid denir. Aslında çoğu sorunun cevabı tanımda yazmaktadır. Eğer ikizkenar ...
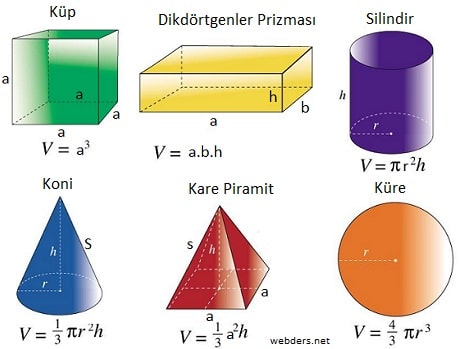
Okumaya devam etHacim Formülü
Geometrik şekillerin hacmi hem geometri dersinde hem de özellikle fizik dersinde çok işimize yarar. Ayrıca kimya dersinde de bazen hacim hesabına ihtiyacımız vardır. Bu yazıda en önemli geometrik şekillerin hacim formülü üzerinde duracağız. Küp, dikdörtgenler prizması, kare prizma, küre, silindir, koni gibi şekillerin hacim formüllerini bilmemiz bize çok şey kazandıracaktır. Şimdi ...
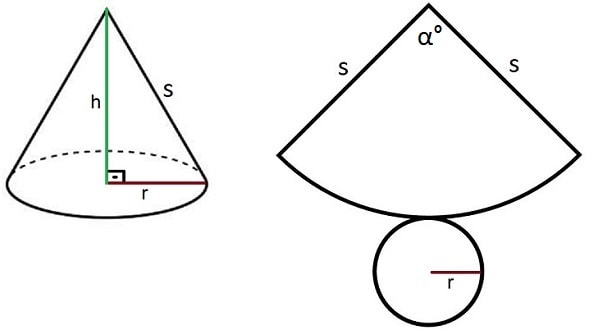
Okumaya devam etKoni Formülleri
Koni üç boyutlu ve sivri ilginç bir cisimdir. Üst üste küçülen daireler koyarsak koni elde ederiz. Koninin en üst kısmı bir nokta, en alt kısmı ise bir dairedir. Bu yazıda koni formülleri üzerinde kısaca duracağız. Daha önce koninin hacmi ve yüzey alanı üzerinde durmuştuk. Koni Açılımı ve Formülleri Koninin formüllerine gelmeden önce koninin ...
Okumaya devam et