Hacim Formülü
Geometrik şekillerin hacmi hem geometri dersinde hem de özellikle fizik dersinde çok işimize yarar. Ayrıca kimya dersinde de bazen hacim hesabına ihtiyacımız vardır. Bu yazıda en önemli geometrik şekillerin hacim formülü üzerinde duracağız.
Küp, dikdörtgenler prizması, kare prizma, küre, silindir, koni gibi şekillerin hacim formüllerini bilmemiz bize çok şey kazandıracaktır. Şimdi tek tek bu şekillerin üzerinde duralım.
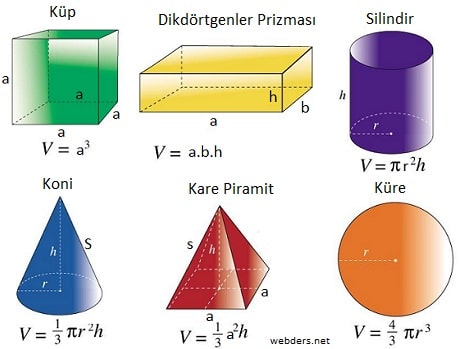
Prizmaların Hacim Formülü
Prizmaları kare prizma, daire prizma (silindir), dikdörtgenler prizması şeklinde sınıflandırabiliriz. Küp ise kare prizmanın özel bir şeklidir. Yani kare prizmanın yüksekliği de taban kenarlarına eşitse o zaman küp elde edilir.
Prizmaların hacmi V = Taban alanı x yükseklik şeklindedir. Bu geometrik şekillerin taban alanlarını veren ifadeler birbirinden farklılık gösterir.
| Cisim | Formül | Açıklama |
|---|---|---|
| Genel olarak prizmalar | A.h | A = taban alanı, h = yükseklik |
| Kare Dik Prizma | V = a2.h | a = karenin taban kenarı, h = prizmanın yüksekliği |
| Küp | a3 = a.a.a | a = küpün bir kenar uzunluğu |
| Dikdörtgen prizma | a.b.h | a, b taban alanının kenarları, h = yükseklik |
| Silindir (dairesel prizma) | π.r2.h | r = taban dairesi yarıçapı, h silindir yüksekliği |
Bu formülleri kullanarak prizmanın hacmini hesaplayabilirsiniz. Örneğin yatay silindir için ekstra bir hacim formülü vermeye gerek yoktur. Aynı formül yatay silindir için de kullanılabilir. Sadece nerenin taban nerenin yükseklik olduğuna dikkat etmek gerekir.
Koni ve Piramit Hacim Formülleri
Bütün kenarlarından çıkan doğruların tepe noktasında birleştiği geometrik şekillere piramit denmektedir Yine geometri dersinde çok sık karşımıza çıkan koni ve piramit formüllerini verelim. Koni de aslında daire piramittir.
Piramitlerde prizmadaki gibi hacim bulunur. Ardından çıkan sonuç 3'e bölünür.
| Cisim | Formül | Açıklama |
|---|---|---|
| Genel olarak piramitler | A.h / 3 | A = taban alanı, h = tabandan tepe noktaya olan dik uzaklık |
| Koni (dairesel tabanlı piramit) | π.r2.h / 3 | r = taban yarıçapı, h = tabandan tepe noktaya olan dik uzaklık |
| Kare piramit | a2.h / 3 | a = karenin bir kenarı, h = tabandan tepe noktaya olan dik uzaklık |
| Dikdörtgen piramit | a.b.h / 3 | a ve b dikdörtgenin kenarları, h = yükseklik |
Piramitler için gereken hacim formüllerini kısaca verdik. Şimdi bir de çok karşımıza çıkan küre hacmini verelim.
Kürenin hacmi V = 4/3.π.r3 formülüyle bulunur. Kürenin hacmi ve yüzey alanı yazısında hem hacme hem de yüzey alanına değinmiştik. Yarım küre sorulduğunda tam kürenin hacmini ikiye bölebilirsiniz.
Etiketler:
Son Eklenenler
- Tarımla İlgili Meslekler
- Matematiği İyi Olmayanlar Hangi Mesleği Seçmeli?
- Antropoloji Nedir?
- Dünyanın Kaç Türlü Hareketi Vardır?
- Toplumsal Düzeni Sağlayan Kurallar Nelerdir?
- Cumhuriyet Yönetiminin Değerleri Nelerdir?
- İklim ve Hava Olayları Arasındaki Fark
- 1 Asal Sayı Mıdır?
- Homeostasi nedir?
- 2 ile Bölünebilme Kuralı
