Dik Üçgen

Geometride üçgenlerin çok önemli bir yeri vardır. Çünkü geometrik şekillerin başlangıcı üçgenlerle olmaktadır. Dik üçgen de özel üçgenler kategorisindeki üçgenlerin ilkidir. Hem açı hem de kenar uzunluklarıyla dik üçgen incelenmeye değerdir. Dik üçgenin alanı özellikle iyi kavranması gereken bir konudur. Bu alana üçgende alan konusu içerisinde gelinecektir. Çünkü ileriki konularda da alan hesaplamalarında aynı bağıntılar kullanılacaktır.

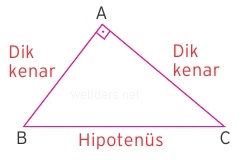
Açılardan birinin ölçüsü 90 derece olan üçgene dik üçgen denir. Dik kenar, hipotenüs ve dik açı işaretini şekil üzerinde anlamak en doğru olandır.

Dik Üçgende Uzunluk

Dik üçgende kenar uzunlukları en temel geometri bağıntısı olan Pisagor bağıntısı ile hesaplanır. Pisagor bağıntısı dik kenar uzunluklarının karelerinin toplamının hipotenüsün uzunluğunun karesine eşit olduğunu ifade eder.

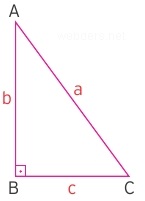
Yukarıdaki dik üçgende Pisagor bağıntısının sonucu olarak a² = b² + c² eşitliği bulunmaktadır. Dolayısıyla b ve c kenarlarının ölçüsünü bildiğimiz zaman doğal olarak a kenarının da ölçüsüne ulaşabiliriz. Ancak bunun için temel düzeyde de olsa kare ve karekök alma işlemlerini yapabiliyor olmamız gerekir.

Pisagor bağıntısı ile ilgili örnek bir soru çözelim.

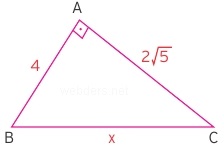
Yukarıdaki üçgende birbirine dik olan iki kenarın uzunluk ölçüleri verilmiştir. En uzun kenar (hipotenüs) x sorulmuştur. Dik kenar ölçülerinin karelerini toplarsak 36 ettiğini görürüz. Bu durumda x uzunluğu 36'nın karekökü olan 6 değerine eşit olur.

Özel Dik Üçgenler

Bazı dik üçgenlerde kenar ölçüleri tam sayılı şekildedir. Bu tür dik üçgenlere özel dik üçgenler denir. Bunları her seferinde hesaplamak yerine ezberden biliriz. Özel dik üçgenlerde en çok bilineni 3,4,5 üçgenidir. Bu üçgen tipinde dik kenarlar 3 ve 4 ile oranlı iken hipotenüs ise 5 ile orantılıdır.

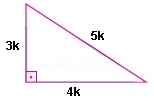
Yukarıdaki modeli verilen 3 4 5 üçgeninde k pozitif sayıları simgeler.

• K = 1 iken 3,4,5 üçgeni
• K = 2 iken 6,8,10 üçgeni
• K = 3 iken 9,12,15 üçgeni
• K = 4 iken 12,16,20 üçgeni
• K = 5 iken 15,20,25 üçgeni olur.

Bu üçgenleri artık hesaplamaya ihtiyaç duymayacak şekilde bilmemiz gerekiyor. Pisagor bağıntısının ürünü olan bu özel üçgeni kendiniz de hesaplayıp test edebilirsiniz.

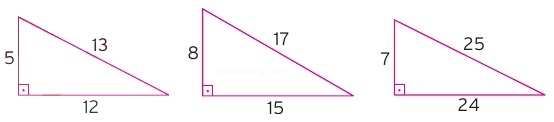
Bunun dışında da en bilinen özel dik üçgenler 5,12,13; 8,15,17; 7,24,25 üçgenleridir. Bu üçgenleri bilmek size pratiklik kazandırır.

Dik Üçgende Öklid Bağıntıları

Bir dik üçgende 90 derecilik açının köşesinden karşı kenara bir dikme indirilirse burada öklid bağıntıları ortaya çıkar. Öklid'in çok uzun zaman önce tespit ettiği bu bağıntılar uzunlukla alakalıdır. Öklid bağıntılarını ancak şekil üzerinde anlayabiliriz.

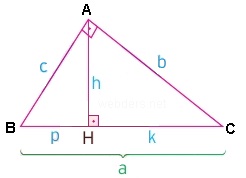
Yukarıda dik köşe içerisinde çıkan dikme ile birlikte öklid koşulları oluşmuş bir üçgen vardır. Bu üçgen üzerindeki harflendirmeler sayesinde öklid'in uzunluk bağıntılarını görebiliriz. Geometride normalde çok fazla formül ezberlenmesi doğru olmamasına rağmen öklid bağıntıları uzunluk açısından çok önemli olduğu için mutlaka bilinmelidir. Öklid'in uzunluk ve yükseklik bağıntılarının hepsi birbiriyle ilgili ve önemlidir.

h² = p.k

b² = k.a

c² = p.a

Bunların dışında Öklid bağıntısı olmamasına rağmen çok kullanılan a.h = b.c bağıntısı da çok önemlidir.

Öklid bağıntıları ile ilgi aşağıdaki örnek soruyu çözelim. Soruda bize Öklid koşulları sağlanmış bir dik üçgende x ile tanımlanmış |BH| kenarının uzunluğu sorulmaktadır.

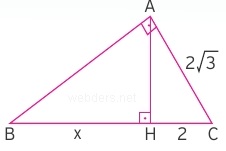
Öklid'in uzunluk bağıntısından 2.(x+2) = |AC|² = 12 olur. Bu basit denklemi çözersek de x = 4 eşitliğini elde ederiz.

Sorunun çözümünü bir adım daha ileri götürüp |AH| kenar uzunluğunu bulalım. Bu kenar yükseklik olduğu için Öklid'in yükseklik bağıntısını kullanırız. Buna göre |AH|² = 2.x olur. Daha önce x = 4 eşitliğini elde etmiştik. Buradan |AH|² = 8 ve |AH| = √8 bulunur.

30 - 60 - 90 Üçgeni

Dik üçgende 90 derecelik bir açının bulunduğunu biliyoruz. Eğer geriye kalan iki açı da 30 ve 60 dereceyse bu dik üçgen özel bir dik üçgen olur. 30 60 90 üçgeninde kenarlar arasına orantısal bir bağıntı bulunur.

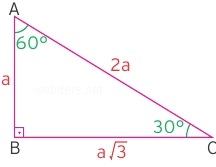
90 derecenin karşısındaki kenar (hipotenüs) 30 derecenin karşısındaki dik kenarın iki katı uzunluktadır. 60 derecenin karşısındaki dik kenar ise 30 derecenin karşısındakinin √3 katı olur.

45 - 45 - 90 Üçgeni

İkizkenar dik üçgen olarak da bilinen 45 - 45 - 90 üçgeni yine özel bir üçgendir. Dik kenarlara bakan açılar eşit olduğu için bu kenarların uzunlukları da eşittir. Hipotenüs ise bu kenarlardan birinin √2 katıdır.

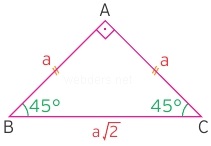
Bir kareyi köşegeninden ikiye ayırırsanız bu üçgenden iki tane elde etmiş olursunuz. Bu üçgen hem şekil itibariyle düzgündür hem de kenar eşitliğiyle bize bazı sorularda çözüm kolaylığı sağlar.

Dik Üçgende Trigonometrik Bağıntılar

Eğer bir üçgende diklik varsa trigonometrik bağıntılar da kurulabilir. Bir x açısının trigonometrik değerleri kenarların birbirine oranıyla tespit edilir. Temel düzeyde 4 tane trigonometrik ifademiz vardır.

Sinx = karşı dik kenar / hipotenüs

Cosx = komşu dik kenar / hipotenüs

Tanx = karşı dik kenar / komşu dik kenar 

Cotx = komşu dik kenar / karşı dik kenar

Temel trigonometrik bağıntılar şekil yardımıyla daha iyi anlaşılabilir. Bir dik üçgende iki açıdan birinin sinüsü diğerinin kosinüsüne eşittir. Birinin tanjantı diğerinin kotanjantına eşittir.

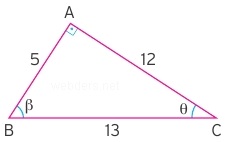
Sinθ = 5/13

Cosθ = 12/13

Tanθ = 5/12

Cotθ = 12/5

Sinβ = 12/13

Cosβ = 5/13

Tanβ = 12/5

Cotβ = 5/12

Yukarıda 5 - 12 - 13 dik üçgeninde gördüğümüz bağıntılardan çeşitli sonuçlar çıkarırız. Daha önce dediğimiz gibi tümler iki açıdan birinin sinüsü diğerinin kosinüsüne eşittir. Aynı ilişki tanjant ve kotanjant arasında da vardır. Aynı şekilde Tan = Sin/Cos ve de Cot = Cos/Sin eşitlikleri de bulunmaktadır.