Açısal Momentum Formülü
Düzgün çembersel hareketle ilgili kavramlardan biri de açısal momentum kavramıdır. Üniversite sınavlarında son yıllarda bu kavramla ilgili sık sık sorular gelmektedir. Bu yazıda açısal momentum formülü üzerinde durmaya çalışacağız.
Her şeyden önce çembersel hareket konusunda eksiğiniz varsa düzgün çembersel hareket konu anlatımı kısmına çalışmanızı öneririz. Orada açısal momentumu da ele aldık.
Açısal Momentum Formülleri ve Birimi
Çembersel hareket formülleri toplu olarak ilgili yazıda verilmişti. Açısal momentum ile ilgili dört ana formül bulunmaktadır. Bunlar aşağıda sıralanmıştır:
- L = r.P
- L = m.v.r
- L = m.ω.r2
- L = I.ω
Bu formüllerin tamamı da bizim için önemlidir. Eğer eylemsizlik momenti verilmişse L = I.ω formülü kullanılabilir. Formüller arasında ilişki kurmak mümkündür. Örneğin çizgisel momentum formülü P = m.v olarak bilinirse ilk formülden ikincisi zaten çıkacaktır.
Açısal momentum formüllerini iyi anlamak için diğer düzgün çembersel hareket formüllerini de bilmeniz faydalı olacaktır.
Açısal Momentum Yönü Bulma
Açısal momentumun yönü sağ el kuralıyla bulunmaktadır. Fizikte manyetizma konusunda da sağ el kuralını kullanmaktayız.
Sağ elimizi kullanarak açısal momentumun yönünü bulabiliriz. Dört parmağımızın yönü dönme yönünü gösterdiği zaman baş parmağımızın ucu açısal momentum vektörünün yönünü gösterir.
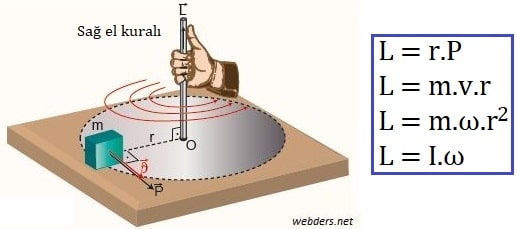
Açısal momentumun mantığını anlamak açısından da yönünü bilmek önemlidir. Örneğin sağdan sola doğru yerde dönen bir cisim yere bir momentum uygular. Bunun aklınıza oturması için vidayı çevirdiğinizde tahtada ilerlemesi olarak da düşünebilirsiniz.
Açısal Momentum Korunumu
Açısal momentum korunumu ilkesi atomik düzeyden gezegenler düzeyine kadar her türlü çembersel hareketi anlamak açısından önemlidir. Bu ilk evrenin her kademesinde geçerlidir.
Sisteme etki yoksa aynı zamanda çizgisel momentumun da korunduğunu biliyoruz.
Bunu bir örnek üzerinden açıklayalım. Güneş sisteminde yörüngesinde dönen bir cisim güneşe yaklaştığı zaman yörünge yarıçapı küçülür. L = m.v.r bağıntısına göre açısal momentumun sabit kalması için r küçüldüğünde m.v'nin büyümesi gerekir. Ancak kütle sabit olduğundan v yani çizgisel hız artar. Biz bunu Güneş'e yaklaşan gezegenin çizgisel hızı artar şeklinde kural olarak öğrenmekteyiz.
Buzda kayan ve gösteri yapan bir sporcu dönme esnasında kollarını kendine doğru kapatır. Bunun nedeni eylemsizlik torkunu küçültmektir. Eylemsizlik torku küçülünce açısal momentumun sabit kalması için dönme hızı artacaktır. Bunu da L = I.ω formülünden çıkarabiliriz.
Etiketler:
Son Eklenenler
- Tarımla İlgili Meslekler
- Matematiği İyi Olmayanlar Hangi Mesleği Seçmeli?
- Antropoloji Nedir?
- Dünyanın Kaç Türlü Hareketi Vardır?
- Toplumsal Düzeni Sağlayan Kurallar Nelerdir?
- Cumhuriyet Yönetiminin Değerleri Nelerdir?
- İklim ve Hava Olayları Arasındaki Fark
- 1 Asal Sayı Mıdır?
- Homeostasi nedir?
- 2 ile Bölünebilme Kuralı
