Çembersel Hareket Formülleri
Düzgün çembersel hareket lise fiziğinin en önemli konularından biridir. Konu anlatımını tamamlamış olsanız bile formülleri toplu olarak görmek tekrar açısından çok işinize yarayacaktır. Unutmayın ki formül ezberlemek bir konuyu öğrenmek için yeterli değildir. Ancak konuyu çalışmaya başlamadan önce veya konuyu bitirdikten sonra formüllere göz gezdirmek konuyu öğrenmek açısından epey fayda sağlayabilir. Çembersel hareket formülleri bu yazıda özet nitelikte derlenmiştir.
Formülleri anlamak için önce bazı temel kavramları belirtmek gerekir.
İlgili yazı: Basit harmonik hareket formülleri
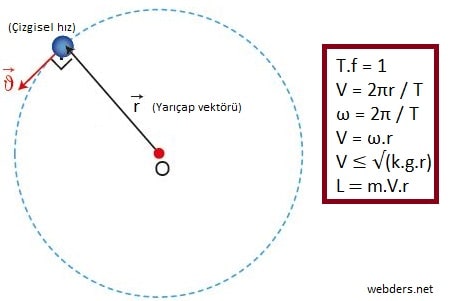
Düzgün Çembersel Harekette Temel Bağıntılar
Yarıçap (r): Düzgün çembersel hareketin yörüngesi ile merkezi arasındaki mesafeye denir. İp ile yapılan çembersel harekette ipin uzunluğu yine yarıçapı verir. Yarıçap r ile gösterilir ve uzunluk olduğu için birimi (m) metredir.
Periyot (T): Düzgün çembersel harekette tam bir turun süresidir. Yani cismin herhangi bir yerden tekrar geçmesi için gereken süredir diyebiliriz. Periyot çok önemli bir kavramdır ve zaman ölçüsü olduğu için birimi (s) saniyedir.
Frekans (f): Periyotun tam tersidir. Bu da 1 saniyede yapılan tur sayısıdır. Periyotun tersi olduğu için birimi de periyotun tersi şeklinde 1/s veya Hertz (Hz) şeklindedir.
Periyot ile frekans arasında bağıntı kurabiliriz. T.f = 1 temel eşitliktir. Öyleyse T = 1 / f ya da f = 1 / T şeklinde eşitlik kurabiliriz. Bu eşitlikler temeldir ve çok önemlidir.
Açısal ve Çizgisel Hız Formülleri
Düzgün çembersel harekette açısal hız, çizgisel hız gibi kavramlar da çok önemlidir. Bu kavramları detaylı öğrenmek için düzgün çembersel hareket konu anlatımı kısmından yararlanabilirsiniz. Burada basitçe formüllerini vereceğiz.
Çizgisel hız (V): Cismin birim zamanda aldığı yolu gösterir. Düzgün bir zeminde hareketteki gibi alınan yolun zamana bölünmesiyle bulunur. Birimi m / s şeklindedir. Çizgisel hız vektörü her zaman yarıçap vektörüne diktir.
Yarıçapı r olan bir yörüngede hareket eden cismin bir tam turda aldığı yol çemberin çevresi kadar yani 2πr şeklindedir. Geçen süre de periyot olduğuna göre V = 2πr / T bağıntısı elde edilecektir. Periyot yerine frekans kullanmak istersek de V = 2πr.f eşitliğini kullanabiliriz.
Açısal hız (ω): Çembersel harekette yarıçapın açı tarama hızıdır. Yani taranan açıyı süreye bölersek açısal hızı elde ederiz. Açısal hızın birimi rad / s (radyan / saniye) şeklindedir. Açısal hız formülü ω = 2π / T veya ω = 2πf şeklindedir.
Açısal hızla alakalı olarak çok merak edilen bir de devir / dakika formülü vardır. Aslında yine mantık aynıdır. Her devir 2π radyan olduğu için ve 1 dakika 60 saniye olduğu için ω = 2π. (devir sayısı) / (dakika x 60) formülü kullanılabilir.
Açısal hız ile çizgisel hız arasında V = ω.r bağıntısı bulunur. Bu bağıntı birçok soru tipinde çok işimize yarayacaktır.
Kuvvet ve İvme Formülleri
Merkezcil kuvvet (F): Bir cismin çembersel hareket yapması için merkeze çeken bir kuvvetin olması gerekir. Merkeze çeken net kuvvete merkezcil kuvvet denir. Kuvvet olduğu için F ile gösterilir ve birimi N (Newton) şeklindedir. Çembersel hareket yapan cismi merkeze çeken kuvvettir. Birimi (N) Newton’dur. F = m.V2 / r formülüyle ifade edilebilir.
Merkezcil ivme (a): Merkezcil kuvvetin etkisiyle merkezcil ivme oluşur. Düzgün çembersel harekette hızın büyüklüğü değişmez ancak yönü değişir. Hızın vektörel olarak değilmesi ivmeyi doğurur. Birimi m / s2 şeklindedir.
Kuvvet ve ivme arasındaki temel bağıntıyı F = m.a olarak ifade edebiliriz. Öyleyse kuvveti kütleye bölersek ivme bulunur. Yani a = V2 / r şeklinde ifade edilir. Eğer açısal hızla ivmeyi ifade etmek istersek V yerine ω.r yazmamız gerekir. Böylece a = ω2.r elde edilir.
Enerji ve Momentum Formülleri
Eylemsizlik momenti (I): Dönen cismin eksene göre oluşturduğu torktur. I sembolüyle gösterilir ve genel olarak I = m.r2 bağıntısıyla ifade edilir. Her cisim için farklılık gösterir.
Dönme kinetik enerjisi (E): Düzgün çembersel harekette dönmeden dolayı bir kinetik enerji ortaya çıkar. E = 1/2.I.ω2 formülü ile ifade edilir.
Açısal momentum (L): Doğrusal ilerleyen bir cismin çizgisel momentumu olduğu gibi dairesel dönen cismin de açısal momentum vardır. Çemberin merkezindedir ve merkeze diktir. Sağ el kuralı ile yönü belirlenir.
Açısal momentum L harfiyle bulunur. Çizgisel momentum ile yarıçap vektörünün çarpımıyla elde edilir. Yani L = r.P olarak ifade edilir. Burada P çizgisel momentumdur. P = m.V olduğu için bu yerine yazarsak L = m.V.r şeklinde genel formül elde edilir. Yine her zamanki gibi çizgisel hız yerine açısal hız yazarsak L = m.ω.r2 eşitliği ortaya çıkar. Eğer eylemsizlik momentumu kullanacaksak da L = I.ω eşitliğinden faydalanabiliriz.
Son olarak dairesel hareket viraj formülleri üzerinde de kısaca duralım. Virajda savrulmadan hareket için V ≤ √(k.g.r) olur. Burada k sürtünme katsayısı g çekim ivmesi ve r virajın yörünge yarıçapıdır. Düşey virajdan güvenli dönüş yapmak için V = √(g.r) olmalıdır. Eğimli virajdan ise savrulmamak için V = √(g.r.tanα) eşitliği kurulur.
Fizik dersi için çok işinize yarayacak çembersel hareket formüllerini ifade ettik. Bunları daha iyi kavramak için çeşitli soru tipleri çözmeli ve bol miktarda tekrar yapmalısınız.
Etiketler:
Son Eklenenler
- Tarımla İlgili Meslekler
- Matematiği İyi Olmayanlar Hangi Mesleği Seçmeli?
- Antropoloji Nedir?
- Dünyanın Kaç Türlü Hareketi Vardır?
- Toplumsal Düzeni Sağlayan Kurallar Nelerdir?
- Cumhuriyet Yönetiminin Değerleri Nelerdir?
- İklim ve Hava Olayları Arasındaki Fark
- 1 Asal Sayı Mıdır?
- Homeostasi nedir?
- 2 ile Bölünebilme Kuralı
