9 İle Bölünebilme Kuralı
Bölünebilme kuralları matematiğin temel konularından biridir. Her seviye matematik sorularında bu kurallar öyle ya da böyle karşımıza çıkmaktadır. 9 ile bölünebilme sorularında kalan soruları da oldukça sık karşımıza çıkmaktadır. Bu yazıda 9 ile bölünebilme kuralı ve ilgili sorular üzerinde duracağız. Konunun mantığını öğrenirsek her türlü soruyu rahatlıkla yapabiliriz.
Her şey bu kadar basit aslında. Rakamların toplamı 9'un katıysa sayı 9'a tam bölünebiliyor demektir. Her şey bu kadar basit olmasına rağmen sınavda çıkan sorularda bazen zorlanabiliyoruz. Bu durumun önüne geçmek için konuyu iyi anlamak ve bol örnek çözmek gerekir.
9'un katlarını düşünelim. 9, 18, 27, 36 şeklinde devam eder. Bu sayıların hepsinin rakamlarının toplamının 9'un katı olduğunu rahatlıkla görebilmekteyiz.
Bölme ve bölünebilme konu anlatımında bölmeyi ve genel olarak bilinmesi gereken bölünebilme kurallarını anlatmıştık. Her sayı için kural farklılık göstermektedir. Ancak şunu söyleyebiliriz ki dokuz ile bölünebilme bunların içerisinde en kolay olanlardan biridir.
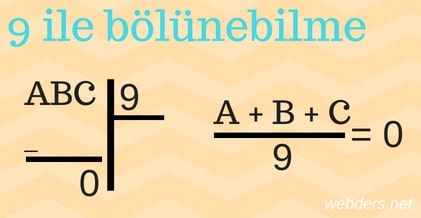
9 İle Bölünebilme Kuralı Soruları ve Cevapları
Kuralı öğrendik. Öyleyse hemen sıcağı sıcağına sorular çözüp bilgimizi pekiştirelim.
Soru #1: 111111111 sayısının dokuz ile bölümünden kalan kaçtır?
A) 0
B) 1
C) 2
D) 3
Çözüm: Gördüğünüz gibi sayı 9 adet 1'den oluşmaktadır. Öyleyse sayının rakamlarının toplamı da 9x1 = 9 olur. Sayının rakamlarının toplamı 9'un katıysa, sayı da 9'un katıdır. Öyleyse sayının 9 ile bölümünden kalan 0 olur. Yani cevap A seçeneğidir.
Soru #2: ABC üç basamaklı sayısı 9 ile tam bölünebilmektedir. Buna göre A + B + C toplamının alabileceği değerlerin toplamı kaçtır?
A) 18
B) 36
C) 54
D) 81
Çözüm: Sayı dokuzun katıysa rakamlarının toplamı da dokuzun katı olacaktır. Öyleyse rakamların toplamı 9, 18, ve 27 olabilir. Ancak 36 olamaz. Çünkü 36 olması için sayılardan en az birinin iki basamaklı olması gerekir. Halbuki ABC sayısı üç basamaklı ise bu üç harf de tek basamaklı olmak zorundadır. Bu nedenle cevap 9 + 18 + 27 = 54 olacaktır. Yani B seçeneği doğrudur.
Soru #3: 361A sayısı 4 basamaklı bir sayıdır. Bu sayının 9 ile bölümünden kalan 3'tür. Buna göre A'nın değeri kaçtır?
A) 0
B) 2
C) 4
D) 6
Çözüm: Sayı tam bölünseydi rakamlarının toplamı 9'un katı olacaktı. Tam bölünmediğine ve kalan 3 olduğuna göre sayının rakamlarının toplamı 9'un katından 3 fazla olmak zorundadır. Rakamları toplarsak 3 + 6 + 1 = 10 olur. 9'un katından 3 fazla olan sayı ise 12 olabilir. Bu durumda A = 2 olmak zorundadır. Cevap B seçeneğidir.
Soru #4: Bir sayı 9'a bölünüyorsa hangisine kesinlikle bölünür?
A) 2
B) 3
C) 4
D) 5
Çözüm: 9 3'ün katıdır. Bu nedenle 9'a tam bölünebilen her sayı 3'e de tam bölünür. Zaten 3 ile bölünebilme kuralı ile 9 ile bölünebilme kuralı aynı şekildedir. Cevap B şıkkıdır.
Merak edenler 7 ile bölünebilme kuralları yazısına da bakabilirler.
9 ile Bölünebilmeyle Alakalı Diğer Bölünebilme Kuralları
Bazen 9 ile bölünebilme şeklinde değil de dokuzun katı olan sayılarla ilgili kalan bulmamız ister. Örneğin 36 ile bölünebilme kuralı buradan gelmektedir. Bu tür durumlarda genel kuralı uygulamamız gerekir.
- Bir sayı hem 9 hem de 2 ile bölünebiliyorsa 18 ile tam bölünür.
- Bir sayı hem 9 hem de 4 ile bölünebiliyorsa 36 ile tam bölünür.
- Bir sayı hem 9 hem de 8 ile bölünebiliyorsa 72 ile tam bölünür.
Bu kuralı uygulayabilmek için çarptığınız iki sayının aralarında asal olması gerekir. Örneğin bir sayı 9 ve 3 ile bölünüyorsa 27'ye de tam bölünür diyemeyiz. Çünkü 9'a bölünebilen her sayı aynı zamanda 3'e de bölünmektedir.
Etiketler:
Son Eklenenler
- Tarımla İlgili Meslekler
- Matematiği İyi Olmayanlar Hangi Mesleği Seçmeli?
- Antropoloji Nedir?
- Dünyanın Kaç Türlü Hareketi Vardır?
- Toplumsal Düzeni Sağlayan Kurallar Nelerdir?
- Cumhuriyet Yönetiminin Değerleri Nelerdir?
- İklim ve Hava Olayları Arasındaki Fark
- 1 Asal Sayı Mıdır?
- Homeostasi nedir?
- 2 ile Bölünebilme Kuralı
