Bölme Bölünebilme

A) Bölme

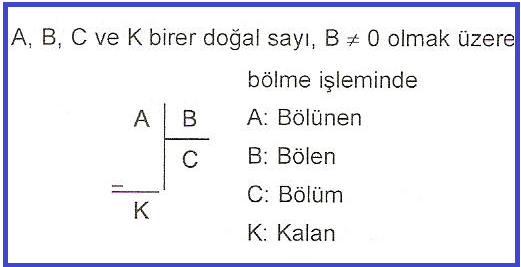
Bölme işleminde;

A = B.C + K  biçiminde gösterilir.

Bir bölme işleminde;

1. K < B dir.
2. K = 0 ise A sayısı B sayısına tam olarak bölünür.
3. Kalan bölümden küçük ise bölen ile bölümün yerlerinin değiştirilmesi kalanı değiştirmez. 

A, B, c, d, e, f, birer tamsayı olmak üzere,

• A nın c ile bölümünden kalan e,
• B nin c ile bölümünden kalan d ise,
• A + B nin  c ile bölümünden kala e + d,
• A - B nin c ile bölümünden kalan e - d,
• A.B nin c ile bölmünden kalan e.d,
• Aⁿ nin c ile bölümünden kalan eⁿ,
• Kalan c den büyükse c ye tekrar bölünmelidir.
• Kalan negatifse kalana pozitif olması için c nin katları eklenmelidir.

Örnek:

13 ile bölündüğünde bölümü 15, kalanı 8 olan sayı kaçtır ?

Çözüm:

İstenen sayıya x diyelim.

x = 13.15 + 8 = 203 tür. 

Örnek:

4ab üç basamaklı bir sayı olmak üzere, 4ab sayısı 26 ile tam bölünebildiğine ve bölüm 17 olduğuna göre, a + b değeri kaçtır ? 

Çözüm:

4ab = 26.17 =442

4ab = 442

Buna göre;

a = 4, b = 2 olduğu için,

a + b = 6 olur.

Bölünebilme Kuralları:

2 ile bölünebilme:

Bölünmek istenen sayının birler basamağı çift ise sayı 2 ye kalansız bölünür. Birler basamağı tek ise sayının 2 ile bölümünden kalan 1 dir.

3 ile bölünebilme:

Bölünmek istenen sayının rakamlarının toplamının 3 ile bölümünden kalan, o sayının 3 ile bölümünden kalana eşittir. Kalan 0 ise o sayı 3 ile tam bölünür.

4 ile bölünebilme:

Bölünmek istenen sayının son iki basamağını oluşturan sayıyının 4 ile bölümünden kalan, o sayının 4 ile bölümünden kalana eşittir. Kalan 0 ise o sayı 4 ile tam bölünüyor demektir.

5 ile bölünebilme:

Birler basamağı 0 yada 5 olan her tam sayı 5 ile kalansız bölünür. Sayının birler basamağının 5 ile bölümünden artan, kalanı verir.

7 ile bölünebilme:

Bölünmek istenen sayının rakamları sağdan sola doğru sırasıyla 1, 3,2 ile çarpılır ve bu çarpımlar üçerli gruplar halinde önce ( + ) ile sonra ( - ) ile çarpılıp toplanır. Toplamın 7 ile bölümünden kalan, sayının 7 ile bölümünden kalana eşittir. Kalan 0 ise sayının 7 ile tam bölündüğü sonucuna ulaşılır.

8 ile bölünebilme:

Bölünmek istenen sayının son üç basamağını oluşturan sayının 8 ile bölümünden kalan, o sayının 8 ile bölümünden kalana eşittir. Kalan 0 ise, o sayı 8 e kalansız bölünüyor demektir.

9 ile bölünebilme:

Bölünmek istenen sayının rakamlarının toplamının 9 ile bölümünden kalan, o sayının 9 ile bölümünden kalana eşittir. Kalan 0 ise o sayı 9 ile kalansız bölünür.

10 ile bölünebilme:

Bölünmek istenen sayının birler basamağındaki rakam, o sayının 10 ile bölümünden kalanı verir. Sayının 10 ile tam bölünebilmesi için birler basamağının 0 olması gerekir.

11 ile bölünebilme:

Bölünmek istenen sayının rakamları sağdan sola doğru +, -, +, -, +, -, ..... ile işaretlendirerek toplanır. Toplamın 11 ile bölümünden kalan, sayının 11 ile bölümünden kalana eşittir.

25 ile bölünebilme:

Bölünmek istenen sayının son iki basamağını oluşturan sayının 25 ile bölümnden kalan, o sayının 25 ile bölümünden kalana eşittir.

* Dikkat edilirse 4, 8, 25 bölünebilme kuralı olarak benzerlik göstermektedir.

** Dikkat edilirse 3 ve 9 bölünebilme kuralı olarak benzerlik göstermektedir.

*** Dikkat edilirse 5 ve 10 bölünebilme kuralı olarak benzerlik göstermektedir.

Aralarında asal sayılara tam bölünebilen sayılar bu sayıların çarpımınada tam bölünür.

• 6 ile tam bölünebilmesi için 2 ve 3 ile,
• 12 ile tam bölünebilmesi için 3 ve 4 ile,
• 15 ile tam bölünebilmesi için 3 ve 5 ile,
• 18 ile tam bölünebilmesi için 2 ve 9 ile,
• 20 ile tam bölünebilmesi için 4 ve 5 ile,
• 24 ile tam bölünebilmesi için 3 ve 8 ile,
• 28 ile tam bölünebilmesi için 4 ve 7 ile,
• 30 ile tam bölünebilmesi için 3 ve 10 yada 5 ve 6 ile tam bölünmesi gerekir.

Örnek:

Beş basamaklı 42736 sayısının 3 ile bölümünden kalanı bulalım.

Çözüm:

4 + 2 + 7 + 3 + 6 = 22

22 nin 3 le bölümünden kalanı bulmalıyız.

2 + 2 = 4

4 ün üç ile bçlümünden kalan 1 dir.

Buna göre 42736 sayısının 3 ile bölümünden kalan 1 dir.

Örnek:

Üç basamaklı 736 sayısının sırasıyla 4, 5, 6, 7, 8, 9, 10, 11, ve 25 ile bölümünden kalanları bulalım.

Çözüm:

• 36 sayısı 4 ün katı olduğu için, 736 sayısının 4 ile bölümünden kalan 0 dır.
• 6 sayısının 5 ile bölümünden kalan bir olduğu için, 736 sayısının 5 ile bölümünden kalan 1 dir.
• 736 sayısı 2 ye tam bölünürken, 3 ile bölümünden 1 kalanını veriyor. 0 dan 5 e kadar olan sayılardan 2 ile tam bölünüp 3 ile bölündüğünde 1 kalanını veren sayı 4 tür. Dolayısıyla 736 sayısının 6 ile bölümünden kalan 4 tür.
• 736 sayısını sırasıyla 1, 3, ve 2 sayıları ile çarpıp toplayıp çıkan sonunucun 7 ile bölümünden kalan, 736 nın 7 ile bölümünden kalana eşittir. (6.1) + (3.3) + (7.2) = 29 ve 29 sayısının 7 ile bölümünden kalan 1 olduğuna göre, 736 nın 7 ile bölümünden kalan 1 dir.
• 736 sayısının 8 ile tam bölünür. Kalan 0 dır.
• (7 + 3 + 6) = 16 olduğundan ve 16 nın 9 ile bölümünden kalan 7 olduğu için 736 sayısının 9 ile bölümünden kalan 7dir.
• 736 sayısının son basamağı 6 olduğu için, 736 sayısının 10 ile bölümünden kalan 6 dır.
• 736 sayısının 11 ile bölümünden kalan (7 + 6) -3 = 10 dur.
• 36 sayısının 25 ile bölümünden kalan 11 olduğu için, 736 sayısının 25 ile bölümünden kalan 11 dir.

Örnek:

634 sayısının 18 ile bölümünden kalan kaçtır ?

Çözüm:

634 sayısı 2 ile tam bölünürken 9 ile bölümünden 4 kalanını veriyor. 0 dan 17 ye kadar olan sayılardan 2 ye tam bölünüp 9 ile bölümünden 4 kalanını veren sayı 4 tür. 634 sayısı 17 ile bölümünden 4 kalanını verir.

Örnek:

120 sayısının asal çarpanlarını bulalım.

Bir Doğal Sayının Tam Bölenleri

Çözüm:

120 = 2³.3.5 tir.

120 nin asal çarpanları 2, 3, ve 5 tir.

Örnek:

2100 sayısının asal çarpanlarını bulalım.

Çözüm:

2100 = 21.100

          = 3.7.10.10

          = 3.7.2.5.2.5 = 2².3.5².7

olduğu için 2100 ün 4 tane asal çarpanı vardır. Bunlar; 2, 3, 5, 7 dir.

Bir Doğal Sayının Tam Bölenlerinin Sayısı

Bir A sayısının asal çarpanlarına ayrılmış şekli;

A = x^a.y^b.z^c olsun.

• A sayısının pozitif tam bölenlerinin sayısı = (a + 1)(b + 1)(c + 1) dir.

• A sayısının tam sayı bölenlerinin sayısı = 2.(a + 1)(b + 1)(c + 1) dir.

• A sayısının tam sayı bölenlerinin toplamı sıfırdır.

• A sayısının asal bölenlerinin sayısı 3 tür. Bunlar x, y, z dir.

Örnek: 

72 sayısının pozitif tam bölenlerinin sayısı kaçtır ?

Çözüm:

72 = 8.9 = 2³.3²

72 nin pozitif tam bölenlerinin sayısı = (3 + 1).(2 + 1) = 12 dir.