İki Kare Farkı
İki kare farkı matematikteki en çok karşımıza çıkan özdeşliklerden biridir. Basit ama çok etkili ve önemlidir. Çarpanlara ayırma konusu matematiğin en önemli konularının başında gelir. Çünkü çarpanlara ayırma konusunu bilmeden matematikteki diğer konularda da işlem yapamayız. Çarpanlara ayırmada işimizi kolaylaştıracak birçok özdeşlik kullanırız. İşte iki kare farkı çarpanlara ayırmadaki en önemli özdeşliktir.
Yani x2 - y2 = (x - y).(x + y) olur.
Bu formül çok basit zaten diye düşünmeyin. Bu özdeşlik o kadar kullanışlıdır ki çok farklı yerlerde karşımıza çıkar. İki kare farkı ile ilgili test sorularında bu özdeşliği hemen göremeyebiliriz. Karesi alınan ifadeler karmaşıklaştıkça soruyu çözmek de zorlaşır. O nedenle bol miktarda soru çözmek gerekir.
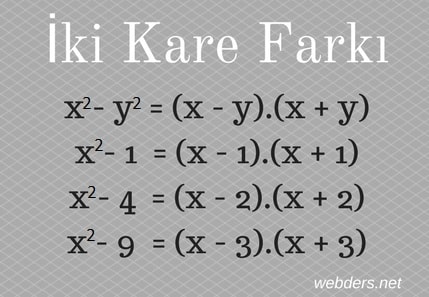
İki Kare Farkı İçin İspat
Örnek sorulara geçmeden önce iki kare farkı özdeşliğinin ispatını yapalım. Böylece kafamıza daha oturmuş olur. İki kare farkında ispat yapmak için iki sayının toplamı ile farkını birbirine çarpmak yeterlidir.
Örneğin a ve b sayılarının farkları ile toplamlarını çarpalım. (a - b).(a + b) = a.a + ab - ba - b.b olur. Bu ifadeyi toparlarsak (a - b).(a + b) = a2 - b2 olacaktır.
Bu şekilde eşitliği unuttuğunuz zaman kendiniz de parantez çarpımı yaparak iki kare farkını elde edebilirsiniz.
Tam kare farkı (a - b)2 = a2 - 2ab + b2 olacaktır. Tam kare farkı ile iki kare farkı karıştırılmamalıdır.
İki Kare Farkı ile İlgili Örnekler
Bu konu çok önemli olmakla birlikte ancak sorular üzerinden iyi öğrenilebilir. Yoksa verilen formülü ezberlemek gayet basittir. Önemli olan bunu kullanabilmektir. Şimdi iki kare farkı ile ilgili örnekler çözelim. Test çözmek bu konuda olmazsa olmazdır.
Soru #1: İki sayının toplamları 20, farkları ise 5'tir. Buna göre bu sayıların karelerinin farkı kaçtır?
A) 4
B) 12,5
C) 20
D) 50
E) 100
Çözüm: Bu soruyu iki ayrı yöntemle çözebiliriz. İlk yöntem toplamları ve farkları verilen sayıları bulmak ve bunların karelerinin farkını almaktır. Bu yöntem biraz uzun olabilir. Çünkü soruda sayıları bulmaya kalktığınızda tam sayı olmadıklarını göreceksiniz. Bu nedenle daha kolay olan iki kare farkı formülünü kullanmalıyız.
Soruda toplamları ve farkları verilen sayıların karelerinin farkı sorulmuş. İki sayının karelerinin farkı zaten toplamları ve farklarının çarpımıyla bulunur. 5.20 = 100 bulunur. Cevap E seçeneğidir.
Soru #2: (x - 3).(x + 3) çarpımı neye eşittir?
A) x + 6
B) x2 + 6
C) x2 - 9
D) x
E) 2x
Çözüm: Formülü yerine koyarsanız cevabı kolaylıkla bulabilirsiniz. Burada birinci sayı x, ikinci sayı ise 3'tür. Karelerinin farkı ise x2 - 9 şeklindedir. Yani cevap C seçeneğidir.
Soru #3: p = √3 + 2 ve q = √3 - 2 olmak üzere p.q çarpımı kaça eşittir?
A) -1
B) 0
C) 1
D) 2
E) 4
Çözüm: p.q çarpımı (√3 + 2).(√3 - 2) şeklindedir. Burada da iki kare farkı vardır. Öyleyse birinci sayının karesinden ikinci sayının karesini çıkarmalıyız. (√3)2 = 3 ve 22 = 4 olduğundan 3 - 4 = -1 bulunur. Doğru yanıt A seçeneğidir.
Soru #4: 49a2 - 4b2 ifadesinin çarpanlarına ayrılmış hali aşağıdakilerden hangisidir?
A) 2a + 49b
B) (7a - 2b).(7a + 2b)
C) (7a - 7b).(2a + 2b)
D) (2a - 2b).(7a + 7b)
E) 7b - 4a
Çözüm: İki kare farkı sorularında kendimize ❝bu neyin karesidir❞ sorusunu sormalıyız. Soruda iki tarafta da kare işareti ve arada da - bulunmaktadır. Öyleyse sorunun iki kare farkı sorusu olduğundan şüphelenmemiz gerekir.
Soruda 49'un kare kökü 7 ve 4'ün de karekökü 2 olduğuna göre ifadeyi (7a)2 - (2a)2 şeklinde düzenleyebiliriz. Öyleyse bu ifadenin çarpanlarına ayrılmış hali (7a - 2b).(7a + 2b) şeklinde olur. Doğru cevap B seçeneğidir.
Bonus:
Çarpanlara ayırma sorularında iki kare farkı kadar yaygın olmasa da iki kare toplamı özdeşliği de bazen karşımıza çıkmaktadır.
İki kare toplamı x2 + y2 = (x + y)2 - 2xy ya da x2 + y2 = (x + y)2 - 2xy olur. Bu formülleri de tam kare eşitliklerinden çıkarırız. Tam kareyi açtığımız zaman (x + y)2 = x2 + y2 + 2xy bulunur. Buradan 2xy ifadesini çıkarırsak geriye iki kare toplamı kalır.
Ek bonus olarak da iki küp farkını verebiliriz. İki küp farkı x3 - y3 = (x - y).(x2 - xy + y2) olur.
Etiketler:
Son Eklenenler
- Tarımla İlgili Meslekler
- Matematiği İyi Olmayanlar Hangi Mesleği Seçmeli?
- Antropoloji Nedir?
- Dünyanın Kaç Türlü Hareketi Vardır?
- Toplumsal Düzeni Sağlayan Kurallar Nelerdir?
- Cumhuriyet Yönetiminin Değerleri Nelerdir?
- İklim ve Hava Olayları Arasındaki Fark
- 1 Asal Sayı Mıdır?
- Homeostasi nedir?
- 2 ile Bölünebilme Kuralı
