Muhteşem Üçlü Teoremi
Geometride çok sık karşımıza çıkan ve işlemlerde büyük kolaylık sağlayan bir kurala değineceğiz. Muhteşem üçlü kuralı ya da muhteşem üçlü teorimi olarak anılan bu özellik dik üçgen söz konusu olduğunda karşımıza çıkmaktadır.
9. sınıf geometri konularında karşımıza çıkan bu kural daha sonraki geometri sorularında da işimize yaramaktadır. Bu nedenle bu kuralı iyi kavramalıyız. Teoremin nereden geldiğini de bilirsek soru içerisinde muhteşem üçlü olduğu zaman kolaylıkla fark ederiz. Bu da bize soruyu daha kolay çözme imkanı verir.
Muhteşem üçlü dik açıdan çıkan kenarortayın böldüğü doğru parçalarına eşit uzunlukta olmasına verilen isimdir.
Geometride bu isimle anılan resmi bir kural yoktur ancak üç doğru parçasının eşit olmasına muhteşem üçlü denmiştir.
Muhteşem Üçlüde Açı ve Kenarlar
Bir dik üçgende dik açıdan hipotenüse kenarortay çizerseniz hipotenüs iki eşit parçaya bölünür. Kenarortayın uzunluğu da bu parçalardan birine eşit olur. Bu şekilde 3 doğru parçası da eşit uzunlukta olur.
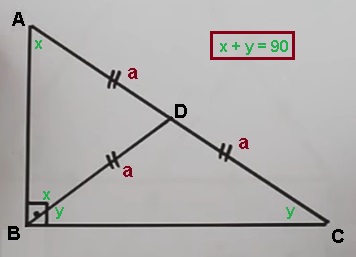
Yukarıdaki şekilde muhteşem üçlü kuralı gösterilmiştir. Görüldüğü gibi dik üçgenin dik kenarından çıkan kenarortay üç tane eşit doğru parçası oluşturmuştur.
Muhteşem üçlü soruları doğrudan bu özelliğin göründüğü şekliyle sorulmayabilir. Çoğunlukla dik açı ve karşısındaki kenar uzunluğu verilir. Burada yapmamız gereken kenarortayı çizerek üç tane eşit yapıyı elde etmektir.
Üçgende ne kadar eşit uzunluk elde edersek açı sorularını da çözmemiz o kadar kolay olur. Çünkü bir üçgende iki eşit kenar ikizkenar üçgen anlamına gelir. Aynı uzunluktaki kenarların karşısına da aynı açılar gelecektir.
Bu konudaki soruları çözerken tecrübeli ve pratik olmak önemlidir. Temel kuralı her zaman uygulayacak bir imkan doğurmalıyız. Dik açı ve karşısında bir kenar gördüğümüz zaman muhteşem üçlüyü ortaya çıkarmak aklımıza direk gelen alternatifler arasında olmalıdır.
Muhteşem Üçlü Kuralının İspatı
Yukarıda da belirtiğimiz gibi kuralın ispatını bilirsek daha doğru kavramış oluruz. Çemberde açı konusunda çapı gören çevre açının 90 derece olduğunu görmüştük. Bu nedenle dik üçgenin köşelerine değecek şekilde bir çember çizersek hipotenüs çap olmak zorundadır.
Çapı ikiye böldüğümüz zaman yarıçap elde ederiz. Kenarortay da çember üzerinden merkeze geldiği için yarıçap olur. Üç tane yarıçapın eşitliği muhteşem üçlüyü ortaya çıkarır.
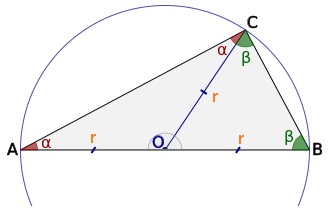
Yukarıdaki şekilde dik üçgenin çevresel çemberi üzerinden muhteşem üçlünün ispatı yapılmıştır. Yarıçapların nasıl ortaya çıktığı da görülmektedir. Dik üçgende bu bağıntıyı gördüğümüz zaman etrafındaki çemberle birlikte hayal etmemiz gerekir. Aslında dik üçgende çevrel çember çok işe yarar bir özelliktir.
Etiketler:
Son Eklenenler
- Tarımla İlgili Meslekler
- Matematiği İyi Olmayanlar Hangi Mesleği Seçmeli?
- Antropoloji Nedir?
- Dünyanın Kaç Türlü Hareketi Vardır?
- Toplumsal Düzeni Sağlayan Kurallar Nelerdir?
- Cumhuriyet Yönetiminin Değerleri Nelerdir?
- İklim ve Hava Olayları Arasındaki Fark
- 1 Asal Sayı Mıdır?
- Homeostasi nedir?
- 2 ile Bölünebilme Kuralı
