Kürenin Hacmi ve Yüzey Alanı
Kürenin yüzey alanı ve hacmine geçmeden önce küreyi tanıyalım.
Çember düzlemde bir noktaya eşit uzaklıktaki noktalar kümesiydi. Daire ise bu noktalar kümesinin iç yüzeyinin tamamıydı. Çember ve daire düzlemde geçerli kavramlardır. Düzlem iki boyutludur. Uzay ise üç boyutludur.
Üç boyutlu uzayda bir noktaya eşit uzaklıktaki noktaların iç bölgesiyle birlikte oluşturduğu geometrik şekle küre denir. Küre bir dairenin üç boyutlu halidir.
Küreye günlük hayatta çok karşılaşırız. Oyun oynadığımız toplar birer küredir. Yediğimiz meyve ve sebzeler tam olarak küre olmasalar da küreye oldukça benzerdirler.
Silindirin hacmi ve yüzey alanı
Kürenin Hacmi
Kürenin hacmini hesaplamak için birden fazla yöntem vardır. Küreyi bir taşırma kabının içerisine atıp da hacmini hesaplayabiliriz. Ancak daha kolay bir yöntem bulunmaktadır.
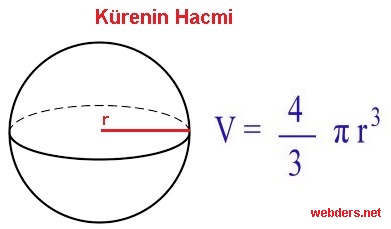
Kürenin hacim formülü V = 4/3.π.r3 şeklindedir.
Öyleyse yarım kürenin hacmini bulmak için bunu iki bölmemiz yetecektir.
Yarım kürenin hacmi 2/3.π.r3 şeklinde ifade edilebilir.
Hemen formülü kullanıp basit bir örnek yapalım.
Soru: Yarıçapı 2 cm olan bir kürenin hacmi ne olur? (π =3)
Çözüm: Formülü aynen uygularız. 4/3.3.23 = 32 cm3 olur.
Formülü bildikten sonra karşımıza çıkacak yarım küre, çeyrek küre gibi geometrik cisimlerin de hacmini rahatlıkla hesaplayabiliriz.
Kürenin hacmini bulurken dikkat etmemiz gerekenlerden biri de yarıçap kullanıyor olmamızdır. Soruda bize bazen çapı verir. Bu durumda işlem yapmadan önce çapı 2’ye bölerek yarıçapı elde etmememiz gerekir.
Kürenin Yüzey Alanı
Küre dairesel bir yapıya sahip olduğu için yüzey alanını doğrudan göremeyebiliriz. O yüzden kürenin yüzey alanı formülünü bilmemiz gerekir.
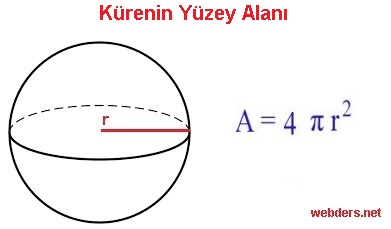
Kürenin yüzey alanı A = 4.π.r2 şeklindedir.
Bu iki formülü aklımda tutamam ve karıştırırım diyorsanız size şöyle bir yöntem sunalım. Eğer basitçe türev almayı biliyorsanız hacmin türevi yüzey alanı verecektir. Hacim formülünün türevini alırsanız yüzey alanı formülü elde edersiniz.
Eğer türev bilmiyorsanız hiç kafanızı karıştırmayın. İki formülü de ezberlemek bu durumda en iyi alternatif.
Kürenin yüzeyi dairesel olduğu için düzleme aktarılamamaktadır. Şekli küreye çok benzer olan Dünya’mızın yüzeyi kâğıda aktarıldığında çeşitli hatalar çıkmaktadır. Bu nedenle birçok harita arasında fark bulunmaktadır.
Kürenin yüzey alanıyla ilgili basit bir örnek yapalım. Demin verdiğimiz örnekteki küreyi kullanalım yine.
Yarıçapı 2 cm olan kürenin yüzey alanı 4.π.22 olur. Eğer π = 3 alırsak cevap 48 cm2 olur.
Şimdi size kafa kurcalayan bir soru soralım. Yarım kürenin yüzey alanı ne olur?
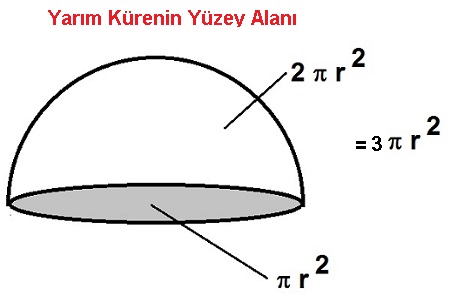
Yarım kürenin hacmini formülü 2'ye bölerek bulduk. Yüzey alanında bunu yapamayız. Çünkü yarım kürenin dış yüzeyinin yanında kesit yüzeyi de vardır.
Yarım kürenin yüzey alanı 2.π.r2 + π.r2 = 3.π.r2 olur.
Kürenin Kesit Alanı
Hacim ve yüzey alanı öğrendikten sonra öğrenmemiz gereken bir diğer alan kürenin kesit alanıdır. Kürenin üzerinden herhangi bir seviyede düzlem şeklinde kesersek ortaya daire şeklinde bir kesit çıkar.
Bu kesit dairenin yarıçapı en fazla kürenin yarıçapı kadar olabilir. Bu da küreyi tam ortadan kestiğimiz durumda gerçekleşir. Karpuzu dilimlemeden önce kapağını kestiğimiz zaman karşımıza çıkan yüzey kürenin kesitine benzetilebilir.
Kürenin kesit alanını bulurken oluşan yeni dairenin yarıçapına ihtiyacımız vardır. Bu yarıçapı bulmak için Pisagor eşitliğini kullanırız.
Bir örnekle kürenin kesit alanını anlamaya çalışalım.
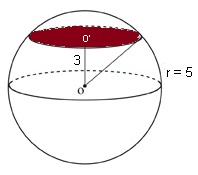
Yukarıdaki şekilde merkezinin 3 birim ötesinde kürenin kesilmesiyle bir kesit alanı oluşmuştur. Bu alanı bulmak için oluşan dairenin yarıçapını bulmamız gerekir. Pisagor bağıntısıyla dik açının karşısında olan kenarın uzunluğu 5 ise, dik kenarlar 3 ve 4 olacaktır.
Öyleyse kesit dairesinin yarıçapı 4 olur.
Dairenin alan formülü π.r2 olduğuna göre kesit alanı da 16π olacaktır.
Etiketler:
Son Eklenenler
- Tarımla İlgili Meslekler
- Matematiği İyi Olmayanlar Hangi Mesleği Seçmeli?
- Antropoloji Nedir?
- Dünyanın Kaç Türlü Hareketi Vardır?
- Toplumsal Düzeni Sağlayan Kurallar Nelerdir?
- Cumhuriyet Yönetiminin Değerleri Nelerdir?
- İklim ve Hava Olayları Arasındaki Fark
- 1 Asal Sayı Mıdır?
- Homeostasi nedir?
- 2 ile Bölünebilme Kuralı
