Silindirin Hacmi Ve Yüzey Alanı
Silindir üç boyutlu, dairesel geometrik şekillerin en bilinenidir. Üst üste daire alanlarının eklenmesiyle silindir meydana gelir. Kalem pil, kupa bardak, kavanoz gibi günlük hayatımızda kullandığımız cisimler silindire birer örnek olarak gösterilebilir.
Silindirin Hacmi
Nasıl ki küpün hacmi hesaplanırken taban alanıyla yüksekliği çarpıyoruz. Silindirde de hacim taban alanı ile yüksekliğin çarpımıdır.
Hacim = taban alanı x yükseklik
V = π.r2.h
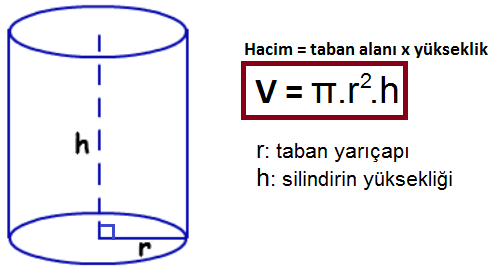
Silindir eşit büyüklükte dairelerin birbirine eklenmesiyle ortaya çıkar. Bu nedenle taban alanı neyse tavan alanı da odur. Formülle taban alanı yerine tavan alanı kullanmak da bir fark oluşturmayacaktır. Silindiri herhangi bir yerinden tabanına paralel bir şekilde kesersek ortaya çıkacak alan yine taban alanına eşittir. Yani silindirin kesit alanı taban alanına eşit olur. Silindir hacmi hesaplarken alan ile yüksekliği çarpmamız yeterlidir.
Silindirin Yüzey Alanı
Silindirin yüzey alanı bir silindirde görülen bütün alanların toplamıdır. Silindirin yüzey alanını bütün alanları toplayarak elde edebiliriz.
Bir silindirde üç tane yüzey vardır: Taban alanı, tavan alanı ve yanal alan.
Yanal alan silindirin alt ve üst yüzeyi dışında kalan alanıdır. Silindir şeklindeki bir bardağı elimizle tuttuğumuz zaman elimizin iç yüzeyinin değdiği yer yanal alandır. Bardağın en altındaki daire şekli taban, bardağın ağzı ise tavan olur.
Yüzey alanı = taban alanı + tavan alanı + yanal alan
Silindirde taban ve tavan zaten aynı olacağından;
Yüzey alanı = 2 x taban alanı + yanal alan
A = 2.π.r2 + 2.π.r.h
Formülde yanal alan yerine 2.π.r.h yazdık. Çünkü yanal alan bu formülle hesaplanır. Yanal alan açıldığı zaman dikdörtgen şeklindi alır. Bu dikdörtgenin bir kenarı h yüksekliği, bir kenarı ise tabanın çevresi yani 2.π.r olur. Silindirde bulunan alanları silindirin açılmış şekliyle daha rahat görebiliriz.
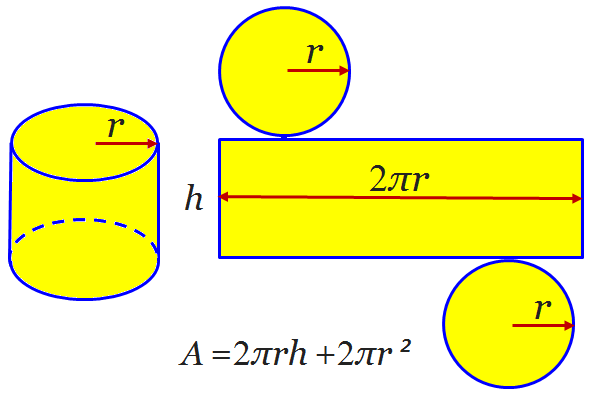
Yukarıdaki şekilde silindirde yüzeyler ve alanların toplamı açık bir şekilde gösterilmiştir.
Dikkat ederseniz formülde 2.π.r ortaktır. İstersek formülü paranteze alma yöntemiyle şöyle yazabiliriz.
A = 2.π.r.(r + h)
Ancak formülün bu hali çok kullanışlı değildir. Formülü ezberlemekten daha önemlisi alan ve hacmi nasıl hesapladığımızı öğrenmiş olmaktır.
Etiketler:
Son Eklenenler
- Tarımla İlgili Meslekler
- Matematiği İyi Olmayanlar Hangi Mesleği Seçmeli?
- Antropoloji Nedir?
- Dünyanın Kaç Türlü Hareketi Vardır?
- Toplumsal Düzeni Sağlayan Kurallar Nelerdir?
- Cumhuriyet Yönetiminin Değerleri Nelerdir?
- İklim ve Hava Olayları Arasındaki Fark
- 1 Asal Sayı Mıdır?
- Homeostasi nedir?
- 2 ile Bölünebilme Kuralı
