Tepe Noktası Bilinen Parabol Denklemi
Parabol konusu matematiğin en önemli konularından biridir. Basit olmasının yanında üniversite sınavlarında mutlaka soru sorulması bu konuyu bizim için daha da önemli hale getirmektedir. Parabol konusunda tepe noktası soruları çok sık sorulmaktadır. Tepe noktası, bir parabolle ilgili bilmemiz gereken en önemli noktadır. Tepe noktası bilinen parabol denklemi yazmak için parabol ile ilgili başka bilgilere de mutlaka sahip olmamız gerekir.
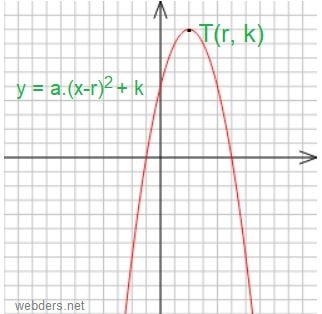
Burada a değeri arttıkça, aynı tepe noktasına sahip parabolün kolları daralır. Eğer a değeri azalırsa parabolün kolları açıktır. a negatifse kollar aşağı doğru, a pozitifse parabolün kolları yukarı doğrudur. Parabol konusunda giriş düzeyinde dahi bilginiz yoksa parabol konu anlatımı kısmından çalışma yapmanızı öneririz.
Eğer parabolümüzün denklemi ax2 + bx + c şeklinde verilmişse, tepe noktasının apsisi -b/2a şeklinde bulunur. Ordinatı ise apsis değeri yerine konularak
Parabolün Tepe Noktası ile İlgili Örnekler
Örnek soru çözerek tepe noktası bilinen bir parabolün denklemi nasıl elde edilir daha iyi öğrenebiliriz.
Soru #1: Tepe noktası T(1, 2) olan parabol y eksenini A(0, 3) noktasında kesmektedir. Buna göre parabolün denklemi aşağıdakilerden hangisidir?
A) y = x2 - 2x + 3
B) y = x2 + 3x + 2
C) y = 2x2 - x + 3
D) y = 4x2 + 2x + 3
E) y = 2x2 - x + 1
Çözüm: Tepe noktası üzerinden parabolümüzü yazalım: y = a(x - 1)2 + 2 şeklinde yazarız. Şimdi de bu parabol 0, 3 noktasından geçtiğine göre bu denklemi sağlaması gerektiğini düşünelim. Öyleyse parabolde x yerine 0 yazarsak y 3'e eşit olacaktır. 3 = a(0 - 1)2 + 2 → 3 = a(-1)2 + 2 → 3 = a + 2 ⇒ a = 1 bulunur.
Şimdi bu a yerine 1 yazarak parabol denklemini elde edelim: y = (x - 1)2 + 2 ⇒ y = x2 - 2x +1 + 2(parantez için karesini aldık) ⇒ y = x2 - 2x + 3 bulunur. Doğru cevap A seçeneğidir. Bu örnek size ilk başta karışık gelse de üzerinde durmakta fayda vardır. Bu soru tipiyle çok sık karşılaşırız.
Soru #2: y = x2 şeklinde verilen bir parabol 3 birim sağa ve 4 birim yukarı öteleniyor. Buna göre ötelenmiş parabol denklemi ne şekilde olur?
A) y = 2x2 - 4x + 5
B) y = x2 + 4x + 5
C) y = x2 - x - 3
D) y = x2 - 6x + 13
E) y = x2 + 3x + 7
Çözüm: Parabolün en saf hali y = x2 şeklindeki paraboldür. Bu parabolün ötelenmesiyle ya da katsayının değiştirilmesiyle diğer bütün paraboller elde edilir. Ötelenmiş parabol denklemi bulmak için tepe noktasının hareketine bakmak gerekir. Tepe noktası ilk başta (0, 0) noktasıyken 3 birim sağa ve 4 birim yukarı ötelenmeyle yeni tepe noktası T(3, 4) noktası olacaktır. Parabolün a katsayısı 1 olarak sabit kalmış ve değişmemiştir.
Bu durumda denklem y = (x - 3)2 + 4 şeklinde bulunur. Parantezin karesini açarsak y = x2 - 6x + 9 + 4 bulunur. Bu da y = x2 - 6x + 13 olur. Cevap D seçeneğidir.
Soru #3: Bir parabolün simetri ekseni x = 3 doğrusudur. Parabolün tepe noktasının orjine olan uzaklığı 5 birim olduğuna göre parabol denklemi aşağıdakilerden hangisi olabilir?
A) y = 2x2 - 3x + 7
B) y = 2x2 - 6x + 7
C) y = x2 - 6x + 13
D) y = x2 + 2x + 6
E) y = x2 + 2x + 4
Çözüm: Parabolde simetri ekseni tepe noktasından geçmektedir. Simetri ekseni x = 3 doğrusu olduğuna göre tepe noktasının apsisi 3 olacaktır. Tepe noktasının orjine olan uzaklığı 5 birim olduğuna göre ordinatı 4 olmalıdır. Bunu 3 4 5 üçgeni için verilen Pisagor bağıntısıyla bulabilirsiniz. Öyleyse tepe noktasının koordinatları T(3, 4) olacaktır. Bu durumda -b / a = 3 olmalıdır. Bunu sağlayan iki seçenek B ve C seçeneğidir.
Ancak parabolde 3 yerine koyduğumuzda 4 değerini elde etmeliyiz. Çünkü tepe noktası parabol üzerinde olduğundan parabolün denklemini de sağlamalıdır. Bunu sağlayan seçenek ise C seçeneğidir. Bu nedenle cevap C seçeneği olacaktır.
Soru #4: Bir parabolün tepe noktasının ordinatı aynı zamanda parabol denkleminin alabileceği en yüksek değer ise bu parabolle ilgili aşağıdakilerden hangisi kesin doğrudur?
A) Parabolün denklemi 3. derecedendir.
B) Parabol y eksenini pozitif tarafta keser.
C) Parabol x eksenini kesmez.
D) Parabolün en küçük değeri de tepe noktasının x eksenine göre simetriğidir.
E) Parabolün kolları aşağı doğrudur.
Çözüm: Parabolün denklemi 3. dereceden olamaz. Parabolün hangi noktayı nereden kestiği ile ilgili kesin bir yargıda bulunamayız. Ancak tepe noktası en yüksek değerse parabolün kolları aşağı inmek zorundadır. Doğru cevap E seçeneğidir.
Tepe noktası ve parabolle ilgili yeteri kadar örnek çözdük. Denemelerde ve kitabınızda karşınıza çıkan parabolleri inceleyerek bilginizi pekiştirebilirsiniz.
Etiketler:
Son Eklenenler
- Tarımla İlgili Meslekler
- Matematiği İyi Olmayanlar Hangi Mesleği Seçmeli?
- Antropoloji Nedir?
- Dünyanın Kaç Türlü Hareketi Vardır?
- Toplumsal Düzeni Sağlayan Kurallar Nelerdir?
- Cumhuriyet Yönetiminin Değerleri Nelerdir?
- İklim ve Hava Olayları Arasındaki Fark
- 1 Asal Sayı Mıdır?
- Homeostasi nedir?
- 2 ile Bölünebilme Kuralı
