Kirişler Dörtgeni
Dörtgenlerin çeşitli özellikleri olduğunu biliyoruz. Çemberin iki noktasını birleştiren doğru parçalarına ise kiriş denir.
Kirişler dörtgeninin ana özelliği karşılıkla açıların toplamının 180 °C olmasıdır. Çemberde açı konusundan da biliyoruz ki çember üzerindeki çember açılar gördükleri yayın yarı ölçüsüne eşittir. Kirişler dörtgeninde karşılıklı iki açı bütün çemberi görmektedir. Yani 360 °C görmektedir. Bu nedenle karşılıklı açıların toplamının da 180 olması gerekir.
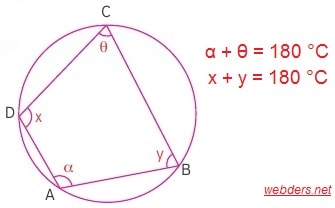
Kirişler dörtgenin diğer bütün özellikleri bu ana özellik üzerinden şekillenmektedir.
Kirişler Dörtgeni İçin Trigonometri Oranları
Kirişler dörtgeninde yukarıda verdiğimiz ana özellikten doğan bir trigonometrik özellik bulunmaktadır. Bu da karşılıklı açılarının sinüslerinin eşit olmasıdır. Çünkü açılardan biri a olduğu zaman diğer açı 180 - a olacaktır. Bütünler açıların sinüsü de eşittir.
Bununla birlikte bu açıların kosinüsleri de zıt işaretlidir. Bütün açıların kosinüsleri arasında sadece işaret farkları vardır. Örneğin:
- Sin40 = sin140,
- Cos30 = -cos150
Bu trigonometrik oranlar kosinüs teorimi ile uzunluk bulma ve sinüs alan formülüyle alan bulma sorularında yaygın olarak kullanılmaktadır.
Bu oranların kirişler dörtgeni içerisinde çeşitli ispatları da mevcuttur. Kirişler dörtgeni için köşegenleri çizip kosinüs teorimini uygularsak sonuca rahatlıkla ulaşırız.
Çemberde Kiriş Özellikleri
Çemberde kirişlerin bize sağladığı bazı özellikler üzerinde kısaca duralım. Çemberde kiriş özellikleri maddeler halinde şöyle sıralanabilir:
- Çemberde eşit uzunluktaki kirişlerin gördükleri yay uzunlukları da birbirine eşittir.
- Uzunluğu eşit olan kirişlerin böldüğü yayların açı ölçüleri de eşittir.
- Eşit uzunluktaki iki kirişin merkeze olan dik uzaklığı da eşittir.
- Merkezden kirişe indirilen dikme ile hipotenüsü yarıçap olan iki adet üçgen çizilir.
- Dört adet kirişin birleştirilmesiyle oluşan dörtgene girişler dörtgeni denir.
Çemberde kiriş özelliklerini iyi bilirsek kirişler dörtgenini özelliklerini de daha iyi kavrarız.
Kirişler Dörtgeni İçin Alan Formülü
Kirişler dörtgeninde alan bulmak için genellikle sinüslü alan formülü kullanılır. Burada köşegen çizilerek dörtgen iki üçgene ayrılır. Sonra her iki üçgende de kirişlerin çarpımı aradaki açısının sinüsüyle çarpılır ve çıkan sonuç 2'ye bölünür.
Ancak aradaki açıyı bilmiyorsak ve dört kirişin uzunluğunu biliyorsan başka bir formül kullanabiliriz. Kirişler dörtgeninin kenar uzunlukları a, b, c, d olsun.
Bu durumda çevre uzunluğu a + b + c + d olur. Çevrenin uzunluğunun yarısına u diyelim. Yani u = (a + b + c + d)/2 olsun.
Alan = √[(u - a)(u - b)(u - c)(u - d)] şeklinde ifade edilir.
Bu alan formülü trigonometrik oranlar kullanılarak ispat edilebilir. Ancak ispatı biraz uzundur.
Kirişler Dörtgeni ile İlgili Çözümlü Sorular
Şimdi de kirişler dörtgeniye ilgili soru çözelim.
Soru #1: Kenar uzunlukları sırasıyla 6, 8, 10 ve 12 birim olan bir kirişler dörtgenin alanı yaklaşık olarak ne kadardır?
A) 76
B) 80
C) 96
D) 102
E) 104
Çözüm: Çevre = 6 + 8 + 10 + 12 = 36 bulunur. Bu durumda u = 36/2 = 18 olur. Şimdi de 18'in kenar uzunluklarına göre farklarını bulalım. Alan = √(18 - 6).(18 - 8).(18 - 10).(18 - 12) = √(12).(10).(8).(6) = √5760 = 75.9 bulunur. Bu da 76'ya çok yakın bir değerdir. Cevap A seçeneğidir.
Soru #2: Bir kirişler dörtgeninde karşılıklı iki açıdan birinin ölçüsü 42 derece olduğuna göre diğerinin ölçüsü kaç derecedir?
A) 48
B) 58
C) 138
D) 142
E) 120
Çözüm: Kirişler dörtgeni soruları çözülürken ilk hatırlanması gereken karşılıklı açıların bütünler olduğudur. Öyleyse karşılıklı açıların toplamı 180 olmak zorundadır. Bir açı 42 ise diğeri de 180 - 42 = 138 bulunur. Cevap C seçeneğidir.
Soru #3: Kirişler dörtgenin bir köşesi 90 °C'lik bir yayı görmektedir. Buna göre bu köşeye komşu olmayan köşedeki açı kaç derecedir?
A) 45
B) 75
C) 90
D) 135
E) 145
Çözüm: Kirişler dörtgenin köşeleri birer çevre açıdır. Çevre açılar gördükleri yayın yarı ölçüsüne sahiptir. Buna göre bu açının ölçüsü 45 °C olur. Bu açıya komşu olmayan açı ise bunun karşı açısıdır. Açılar karşılıklı bütünler olduğundan karşı açının ölçüsü 180 - 45 = 135 °C bulunur. Doğru cevap D seçeneğidir.
Etiketler:
Son Eklenenler
- Tarımla İlgili Meslekler
- Matematiği İyi Olmayanlar Hangi Mesleği Seçmeli?
- Antropoloji Nedir?
- Dünyanın Kaç Türlü Hareketi Vardır?
- Toplumsal Düzeni Sağlayan Kurallar Nelerdir?
- Cumhuriyet Yönetiminin Değerleri Nelerdir?
- İklim ve Hava Olayları Arasındaki Fark
- 1 Asal Sayı Mıdır?
- Homeostasi nedir?
- 2 ile Bölünebilme Kuralı
