İki Kare Toplamı
Çarpanlara ayırma konusunda birçok özdeşlik görmekteyiz. Bu özdeşlikler sayesinde matematik sorularını daha kolay hale getirip çözme imkanına sahip olmaktayız. İki kare toplamı bu özdeşliklerden biridir. Daha önce iki kare farkı adlı yazıda iki kare farkını örnek sorularla anlatmıştık. Bu yazıda ise iki kare toplamı üzerinde duracağız.
İki kare farkı özdeşliği: x2 - y2 = (x - y).(x + y)
İki kare toplamı özdeşliği: x2 + y2 = (x + y)2 - 2xy = (x - y)2 + 2xy
Burada dikkat edilmesi gereken şey iki kare toplamı ile tam kare toplamının aynı olmadığıdır. Biri iki sayının karelerinin toplanması iken diğeri iki sayının toplamının karesidir.
Örneğin 4 ile 1'in karelerini toplarsak 16 + 1 = 17 olur. Ancak bu sayıları toplayıp karelerini alırsak (4 + 1)2 = 25 olur. Görüldüğü gibi ikisi birbirinden farklıdır.
İşte iki kare toplamı formülü bu ikisi arasında ilişki kurmak içindir. İki kare toplamını tam kare toplamı veya tam kare farkı kullanarak elde edebiliriz. Bunun dışında iki kare toplamının iki kare farkı gibi basit bir formülü yoktur.
İki Kare Toplamının Elde Edilmesi
Yukarıda da belirttiğimiz gibi bu özdeşlik tam kare farkı veya tam kare toplamı özdeşliğinden elde edilmektedir. Şimdi parantez içine alıp kare almak ile ayrı ayrı kare almak arasındaki ilişkiden farkı görelim.
(x + y)2 = x2 + y2 + 2xy olur. Bu matematikte en çok kullanılan tam kare özdeşliğidir. Eğer özdeşliğin sağlamasını paranteze dağıtarak çarpma yoluyla da yapabilirsiniz.
Şimdi burada x2 + y2 ifadesini yalnız bırakmak için her iki taraftan 2xy ifadesini çıkarmamız gerekir.
Bu durumda (x + y)2 - 2xy = x2 + y2 olacaktır.
Aynısını tam kare farkı için de uygulayabiliriz. Bu sefer tam kareye 2xy eklemek yerine çıkarırız.
(x - y)2 = x2 + y2 - 2xy olur. Her iki tarafa 2xy eklersek de (x - y)2 + 2xy = x2 + y2 olacaktır.
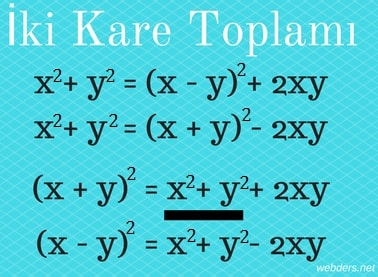
İki Kare Toplamı ile İlgili Örnekler
İki kare toplamı ile ilgili örnek sorular çözerek öğrendiğimiz basit şeyleri pekiştirelim.
Soru #1: a ve b iki reel sayı olmak üzere a + b = 8 ve a.b = 5 eşitlikleri verilmiştir. Buna göre a2 + b2 ifadesinin değeri kaçtır?
A) 54
B) 56
C) 58
D) 60
E) 64
Çözüm: Soruda sayıların toplamı verilmiştir. Bu toplamın karesini alırsak (a + b)2 = 82 = 64 olur. Şimdi bu ifadeden 2ab ifadesini çıkaralım. 2.5 = 10 olduğuna göre a2 + b2 = 64 - 10 = 54 bulunur. Doğru yanıt A seçeneğidir.
Soru #2: İki sayının farkı 10, karelerinin farkı ise 120'dir. Buna göre bu sayıların karelerinin toplamı kaçtır?
A) 119
B) 120
C) 121
D) 122
E) 123
Çözüm: İki sayıya x ve y diyelim. Bu durumda x - y = 10 ve x2 - y2 = 120 olacaktır. İki kare farkından x2 - y2 = (x - y).(x + y) olduğunu biliyoruz. Öyleyse 120 = 10.(x + y) olur. Buradan da x + y = 12 bulunur.
Şimdi iki denklemi kullanarak x ve y sayılarını bulalım. x - y = 10 ve x + y = 12 denklemlerini toplarsak 2x = 22 ve x = 11 bulunur. Bu durumda y de 1 olur. Öyleyse karelerin toplamı 112 + 12 = 121 + 1 = 122 bulunur. Cevap D seçeneğidir.
Soru #3: a + 1/a = 7 ise a2 + 1/a2 kaçtır?
A) 45
B) 47
C) 49
D) 51
E) 63
Çözüm: a + 1/a ifadesinin karesini alalım. Bu durumda (a + 1/a)2 = 49 = ;a2 + 1/a2 + 2.a.1/a olur. 2.a.1/a = 2 olduğuna göre 49 = a2 + 1/a2 + 2 bulunur. Burada 2'yi diğer tarafa atarsak, a2 + 1/a2 = 47 bulunur. Cevap B seçeneğidir.
Bonus: Üç Kare Toplamı
İki kare toplamını ele aldık. Şimdi de bonus olarak üç kare toplamını verelim.
Üç kare toplamı a2 + b2 + c2 = (a + b + c)2 - 2(ab + ac + bc) şeklinde ifade edilebilir.
Aslında bunun da temel çıkış noktası aynıdır. (a + b + c)2 = a2 + b2 + c2 + 2ab + 2ac + 2bc şeklindedir. Burada da kareli ifadeleri elde etmek için çarpımlı ifadeleri çıkarmak gerekir.
Etiketler:
Son Eklenenler
- Tarımla İlgili Meslekler
- Matematiği İyi Olmayanlar Hangi Mesleği Seçmeli?
- Antropoloji Nedir?
- Dünyanın Kaç Türlü Hareketi Vardır?
- Toplumsal Düzeni Sağlayan Kurallar Nelerdir?
- Cumhuriyet Yönetiminin Değerleri Nelerdir?
- İklim ve Hava Olayları Arasındaki Fark
- 1 Asal Sayı Mıdır?
- Homeostasi nedir?
- 2 ile Bölünebilme Kuralı
