Bir Noktası ve Eğimi Bilinen Doğru Denklemi
Analitik geometride doğru denklemleri çok önemlidir. Doğru denklemi konusunda doğrunun denkleminin nasıl bulunduğunu geniş olarak ele aldık.
Bir doğrunun denklemini bulabilmek için iki bilgiye ihtiyacımız vardır. Bunlar:
- Doğrunun eğimi
- Doğrunun üzerindeki herhangi bir nokta
Şeklindedir.
Dolaysıyla eğimi ve bir noktası bilinen doğru denklemini bulma en doğal şeydir. Zaten ihtiyacımız olan şey sadece bu ikisidir.
Geometride eğim m harfiyle ifade edilir. Buna göre A(x1 , y1) noktasından geçen ve eğimi m olan bir doğrunun denklemi m = (y - y1) / (x - x1) formülü ile elde edilir. Bu formül aslında eğimin nasıl bulunduğunu da ortaya koymaktadır. İki noktanın ordinatları (y) farkını apsisler (x) farkına bölerseniz eğimi elde edersiniz.
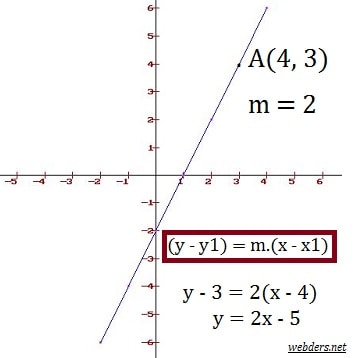
Eğer doğruda eğim verilmemiş ve bunun yerine iki nokta verilmişse bu durumda da iki noktadan eğimi bulur ve yine herhangi bir noktayla denklemi elde ederiz. Şimdi verdiğimiz formülle ilgili örnekler yapalım.
Bir Noktası ve Eğimi Bilinen Doğru Denklemi Soruları
Soru: Eğimi 3 ve A(2, 4) noktasından geçen doğrunun denklemi nedir?
Çözüm: Yukarıdaki formülü aynen yazalım: 3 = (y - 4) / (x - 2) ⇒ (y - 4) = 3.(x - 2) şeklinde de yazılabilir. Buradan da y - 4 = 3x - 6 bulunur.
Bulunan eşitliği iki türlü de düzeltip denklem elde edebiliriz. Sağdakileri sola işaret değiştirerek atarsak y - 3x + 2 = 0 şeklinde doğru denklemini elde ederiz.
Denklem için y'yi yalnız bırakırsak da y = 3x - 2 şeklinde denklem bulunur. Bu iki denklem de aynıdır. İkisinde de A(2, 4) noktasını yerine yazdığımızda denklem bunu noktayı sağlar.
Soru: A(1, 3) ve B(2, 5) noktalarından geçen doğru denklemini hangisidir?
Çözüm: Soruda bize iki nokta verilmiştir. Ancak ihtiyacımız olan bir nokta ve bir de eğimdir. Öyleyse iki noktası verilen doğruda eğim bulalım. Sonra da elimizdeki iki noktadan biriyle denklemi yazalım.
Eğim m = (5 - 3) / (2 - 1) = 2/1 = 2 bulunur. Şimdi de iki noktadan herhangi biriyle denklemi yazalım. Örneğin A noktasıyla denklemi yazarsak (y - 3) = 2.(x - 1) ⇒ y - 3 = 2x -2 ⇒ y = 2x + 2 olarak ifade edilir. Eğer denklemi 0'a eşitlenmiş şekilde yazmak istersek de hepsini bir tarafta toplayıp y - 2x - 2 = 0 olarak elde ederiz.
İsterseniz bulunan bu eğimle B noktasını kullanarak siz de denklemi yazmayı deneyin. Sonucun aynı olduğunu göreceksiniz.
Etiketler:
Son Eklenenler
- Tarımla İlgili Meslekler
- Matematiği İyi Olmayanlar Hangi Mesleği Seçmeli?
- Antropoloji Nedir?
- Dünyanın Kaç Türlü Hareketi Vardır?
- Toplumsal Düzeni Sağlayan Kurallar Nelerdir?
- Cumhuriyet Yönetiminin Değerleri Nelerdir?
- İklim ve Hava Olayları Arasındaki Fark
- 1 Asal Sayı Mıdır?
- Homeostasi nedir?
- 2 ile Bölünebilme Kuralı
