İki Nokta Arası Uzaklık
10. sınıf geometri müfredatında karşımıza çıkan iki nokta arası uzaklık bulma soruları ilerleyen analitik geometri konuları için de önemlidir. Koordinat sisteminde iki nokta arasındaki uzaklığı ya da iki noktanın ortak noktasını bulmayı iyi öğrenirsek birçok problemi daha iyi çözebiliriz.
Bu yazıda bu konuyu basitleştirerek anlatacağız. Ardından örnek sorular ile bilgimizi pekiştireceğiz. Matematik ve geometride en basit konuyu bile hafife almadan detaylı olarak çalışmamız gerektiğini unutmamalısınız.
İki Nokta Arası Uzaklık Hesaplama Formülü
Sorularda bazen koordinat sistemi üzerinde belirtilen noktalar ile uzaklık hesaplamamızı ister. Bazen de noktaların sadece yerlerini anlatıp soru sorar. Her iki durum da kullanacağımız bağıntı Pisagor bağıntısıdır.
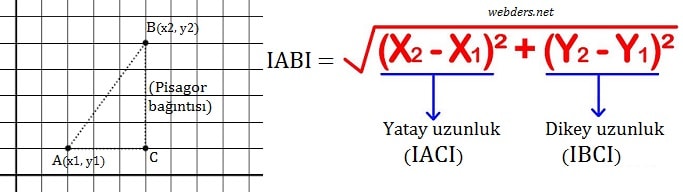
Yukarıdaki şekilde iki nokta arasındaki uzaklık hem geometri bilgisiyle hem de formülü kullanılarak bulunmuştur. Aslında formül de Pisagor teoreminin uygulamasından gelmektedir. Yani formül uygulamak yerine çizerek de hesaplama yapabilirsiniz. Ancak çok örnek çözdüğünüzde artık çizmeye gerek kalmadan hesaplama yapabilirsiniz.
A ve B noktaları arasındaki uzaklık IABI = √((x2 - x1)2 + (y2 - y1)2) formülü ile bulunur. Formül kafanızı karıştırmasın çünkü basitçe apsis ve ordinatların (x ve y'lerin) farklarının karesini toplayıp, ardından karekök alıyoruz. Olay bu kadar basit aslında.
Noktalar Arası Uzaklık Soruları ve Çözümleri
Örnek sorular ve çözümleri ile yukarıdaki formülü nasıl kullandığımızı görelim.
Soru: Koordinat düzlemindeki A(1, 2) ve B(4, 6) noktaları arasındaki uzaklık kaç birim olur?
Çözüm: İki noktanın apsisleri 1 ve 4, ordinatları ise 2 ve 6'dır. 4 - 1 = 3 ve 6 - 2 = 4 olur. Aralardaki farkın karelerini toplayıp sonra karekök alırsak IABI = √(32 + 42) = √25 = 5 bulunur.
Soru: K(3, -1) noktası ile L(5, 6) noktaları birleştirilerek IKLI doğru parçası oluşturuluyor. Buna göre bu doğru parçasının uzunluğunu hesaplayınız.
Çözüm: Soruda iki nokta arasındaki uzaklığı hesaplamamızı istemektedir. Apsisler farkına ve ordinatlar farkına bakalım. 5 - 3 = 2 ve 6 - (-1) = 7 bulunur. Bunların karelerini alıp toplarsak 22 + 72 = 4 + 49 = 53 bulunur. Sonra da bunun karekökünü alalım: IKLI = √53 birim bulunur.
İki Nokta Arasındaki Orta Nokta
Bazen sorularda noktalar arasındaki uzaklığı değil de iki noktanın orta noktasını sorar. Bu durumda apsis ve ordinatların orta noktasını sırayla yazmanız yeterlidir. Bunun için de aritmetik ortalama kullanılır.
Örneğin (2, 2) ile (4, 4) noktasının orta noktası doğal olarak (3, 3) noktası olacaktır. Burada apsislerin aritmetik ortalamasını ve ordinatların ortalamasını ayrı ayrı alırız.
Soru: A(1, 6) noktası ile B(7, -2) noktasının tam ortasında C noktası vardır. Buna göre C noktasının koordinatlarını bulunuz.
Çözüm: C(x, y) olsun. Bu durumda x = (1 + 7) / 2 = 4 ve y = (6 + (-2)) / 2 = 2 bulunur. Demek ki C noktasının koordinatları (4, 2) şeklindedir. Gördüğünüz gibi yaptığımız tek şey işaretine bakmadan orta nokta almaktadır.
Etiketler:
Son Eklenenler
- Tarımla İlgili Meslekler
- Matematiği İyi Olmayanlar Hangi Mesleği Seçmeli?
- Antropoloji Nedir?
- Dünyanın Kaç Türlü Hareketi Vardır?
- Toplumsal Düzeni Sağlayan Kurallar Nelerdir?
- Cumhuriyet Yönetiminin Değerleri Nelerdir?
- İklim ve Hava Olayları Arasındaki Fark
- 1 Asal Sayı Mıdır?
- Homeostasi nedir?
- 2 ile Bölünebilme Kuralı
