Parabol Denklemi Yazma
Parabol konusunda grafiği verilen bir parabolün denklemini yazabilmek önemlidir. Birçok öğrenci bu konuda sıkıntı yaşamaktadır. Eğer grafiği verilen bir parabolün denklemini yazabiliyorsak bunun tersini de yapabiliriz. Yani denklemden parabolün nasıl bir şekli olduğunu kendimiz çizebiliriz.
Parabolün denklemini yazmak için elimizde bazı bilgilerin olması gerekir. Bu bilgiler bazen yazılı olarak verilir. Bazen de grafik üzerinden bunları elde edebiliriz.
Burada iki önemli bilgi işimize yarayacaktır.
- Prabolün eksenleri kestiği noktalar
- Parabolün tepe noktası
Şimdi bunları tek tek ele alalım.
Eksenleri Kestiği Noktaları Bilinen Parabolün Denklemi
Parabol genellikle x eksenini 2 noktada ve y eksenini 1 noktada keser. Parabolün x eksenini kestiği noktalar parabolün kökleridir. Yani bu noktaları denklemde yerine yazarsanız sonuç 0 çıkacaktır. Çünkü bı noktaların y değeri 0'dır.
Parabol üzerindeki her noktanın parabol denklemini sağlamak zorunda olduğunu unutmayın.
Apsis yani x eksenini kestiği noktaları bilinen parabolün denklemi y = a.(x - x1).(x - x2) olur. Burada x1 ve x2 x ekseninin kesildiği noktalardır. Dikkat ederseniz bu noktaları yazarsak denklemin sonucu 0 olmaktadır.
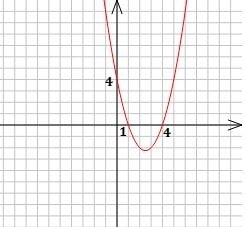
Yukarıdaki parabol denkleminde grafik x eksenini (1, 0) ve (4, 0) noktasından kesmektedir. Buna göre denklemin basit hali y = a(x - 1).(x - 4) olacaktır. Burada a bir katsayıdır ve grafiğin kolları arasındaki darlık ve genişliği ifade eder.
Denklemde a'yı da bulmak için y ekseninin kesildiği noktayı denklemin yerine yazalım. Bu noktada x = 0 ve y = 4 olmaktadır. Öyleyse 4 = a.(0 - 1).(0 - 4) ⇒ 4 = 4a ⇒ a = 1 olacaktır.
Parabolün denklemi de y = 1.(x - 1).(x - 4) ⇒ y = x2 - 5x + 4 bulunacaktır.
Paraboller ikinci dereceden denklemlerin grafiğe aktarılmış halleridir. Bu nedenle y = ax2 + bx + c şeklinde yazılabilirler. Burada c noktası her zaman y ekseninin kesildiği nokta olacaktır. Örneğimizde de bu şekilde yer almıştır.
Tepe Noktası Bilinen Parabolün Denklemini Yazma
Bazı durumlarda parabolün denklemini bilmeyiz fakat tepe noktasını biliriz. Tepe noktasının biri x, diğeri y ekseninden olmak üzere iki nokta ile ifade edildiğini biliyoruz. Bu noktalara r ve k dersek tepe noktası T(r, k) şeklinde ifade edilir.
Tepe noktası T(r, k) olan bir parabolün denklemi de y = a.(x - r)2 + k şeklinde ifade edilir. Burada parabolün en saf hali olan y = x2 şeklinden hangi yöne ne kadar ötelendiği anlatılmaktadır.
Kare alma işlemini yapıp denklemi açarsak eğer denklem yine y = ax2 + bx + c formuna gelecektir.
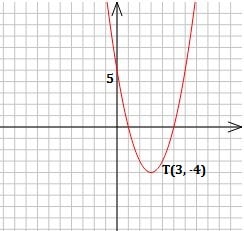
Yukarıda parabolde tepe noktası T(3, -4) şeklinde verilmiştir. Öyleyse y = a.(x - 3)2 - 4 şeklinde denklem yazılabilir. Denklem aynı zamanda y eksenini (0, 5) noktasında kestiği için bu noktayı yerine koyabiliriz. Öyleyse 5 = a(0 - 3)2 - 4 ⇒ 5 = 9a - 4 ⇒ 9 = 9a ⇒ a = 1 bulunur.
Bu durumda denklemi açarsak y = 1.(x - 3)2 - 4 ⇒ y = x2 - 6x + 5 bulunacaktır. Görüldüğü gibi denklemin sabit sayısı (c noktası) yine y ekseninin kesildiği nokta olmaktadır.
Parabol denklemlerini yazmak ve parabol grafiklerini çizmek için bol miktarda örnek yapmak gerekir. Soru çözdükçe konu kolaylaşacaktır. Parabol konu anlatımı kısmından konuya detaylıca çalışabilirsiniz.
Etiketler:
Son Eklenenler
- Tarımla İlgili Meslekler
- Matematiği İyi Olmayanlar Hangi Mesleği Seçmeli?
- Antropoloji Nedir?
- Dünyanın Kaç Türlü Hareketi Vardır?
- Toplumsal Düzeni Sağlayan Kurallar Nelerdir?
- Cumhuriyet Yönetiminin Değerleri Nelerdir?
- İklim ve Hava Olayları Arasındaki Fark
- 1 Asal Sayı Mıdır?
- Homeostasi nedir?
- 2 ile Bölünebilme Kuralı
