Stewart Teoremi
Bu yazıda geometri sorularında işimizi kolaylaştıracak bir teorem üzeride duracağız. Öncelikle Stewart Teoremi ne işe yarar onu söyleyelim. Bir üçgenin köşelerinden birinden karşı kenara çizdiğiniz herhangi bir doğru parçasının uzunluğunu Stewart teoremi ile kolayca bulabiliriz.
Teoremin güzelliği ise herhangi bir açı veya özel durum gerektirmemesidir. Her koşulda geçerli bu teoremi öğrenmeden önce Stewart Teoremi ile ilgili kim buldu sorusunu cevaplayalım. Bildiğimiz gibi teoremlere genellikle onu ortaya koyan kişinin adı verilir. Stewart teoremi ise Ian Stewart tarafından bulunmuştur. Ian Stewart 24 Eylül 1945 doğumludur. Yani bu teorem öyle yüzlerce yıl önce bulunmuş değildir.
Stewart Teoremi Formülü ve Özellikleri
Şimdi önce şekil üzerinde formülü gösterelim. Ardından örnek soru da çözerek bazı özellikleri öğrenelim.
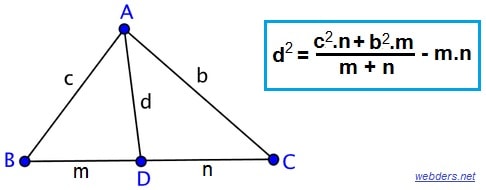
Yukarıdaki görselde Stewart teoremi basitçe özetlenmiş ve formülü de verilmiştir. Bu formülü ezberlemek ilk başta biraz zor görünse de birkaç tane soruyu çözmeyi denerseniz o kadar da zor olmadığını görürsünüz.
Üçgenin köşesinden karşı kenara çizilen doğru parçasına d dersek, d2 = (c2.n + b2.m) / (m + n) - m.n olur.
Formülü daha iyi hatırlamak için c ile n'nin ve b ile m'nin çapraz olduğuna dikkat ediniz. Yukarıdakilerin karesi ile aşağıdaki çaprazın normal halini çarpıyoruz. Sonrada aşağıdakilerin toplamına bölüyoruz. Ardından aşağıdakilerin çarpımını çıkarıyoruz.
Stewart Teoremi ile İlgili Çözümlü Sorular
Üçgende bir köşeden çizdiğimiz doğru parçası eğer yükseklikse Pisagor bağıntısı kullanabiliriz. Ya da kenarortaysa onunla ilgili özellikleri kullanırız. Ancak elimizde hiçbir bilgi yoksa o zaman bu teorem hayat kurtarır. Çünkü her koşulda işe yaramaktadır. Şimdi bir soru çözerek öğrendiğimizi pekiştirelim.
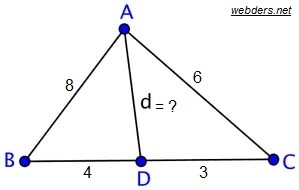
Örnek: Yukarıdaki üçgende verilen ölçülere göre d uzunluğu kaç birim olur?
Çözüm: Yapmamız gereken şey formülü uygulamaktadır. Formüle göre d2 = 82.3 + 62.4 / (4 + 3) - (4.3) olacaktır. Buradan da d2 = 336 / 7 - 12 = 36 ⇒ d = 6 birim bulunacaktır.
Stewart Teoreminin İspatı
Teoremin ispatını günlük hayatta çok kullanmasak da yine de verelim. Bir şeyin nereden geldiğini bilirsek onu daha iyi kavramış oluruz. Stewart teoreminin ispatı kosinüs teoreminden ya da yükseklik çizilerek de yapılabilir. İşlemler biraz karışık olduğundan ispata merakı olan arkadaşların biraz zaman ayırması gerekecektir.
Önce yukarıdaki gösterime bir de yükseklik ekleyelim. Ardından da Pisagor bağıntılarını yazalım.
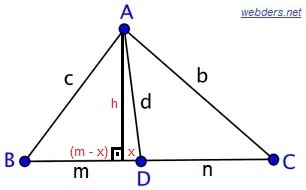
En temel üç Pisagor bağıntımızı yazalım.
- b2 = h2 + (n + x)2
- c2 = h2 + (m - x)2
- d2 = h2 + x2
İlk eşitliği m ile, ikincisini de n ile genişletip ardından taraf tarafa toplayalım.
- b2m = h2m + n2m + 2mnx + x2m
- c2n = h2n + m2n − 2mnx + x2n
Toplarsak eğer;
b2m + c2n = (m + n)(h2 + mn + x2) = (m + n)(d2 + mn) bulunur.
Buradan da (m + n) karşıya bölüm olarak atılırsa;
(d2 + mn) = (b2m + c2n) / (m + n) olur. Ardından da m.n karşı tarafa eksi olarak atılır ve formül elde edilir:
d2 = (c2.n + b2.m) / (m + n) - m.n
Dediğimiz gibi ispat biraz kafa karıştırabilir ama Pisagor yöntemiyle denerseniz kendiniz de bulursunuz. Kosinüs teoremi ile de ispat yapılabilir ancak bu yöntem daha akla yatkın çünkü kosinüs teoreminin formülünü unutabilirsiniz.
Etiketler:
Son Eklenenler
- Tarımla İlgili Meslekler
- Matematiği İyi Olmayanlar Hangi Mesleği Seçmeli?
- Antropoloji Nedir?
- Dünyanın Kaç Türlü Hareketi Vardır?
- Toplumsal Düzeni Sağlayan Kurallar Nelerdir?
- Cumhuriyet Yönetiminin Değerleri Nelerdir?
- İklim ve Hava Olayları Arasındaki Fark
- 1 Asal Sayı Mıdır?
- Homeostasi nedir?
- 2 ile Bölünebilme Kuralı
