Düzgün Dörtyüzlü
Geometri dersinde karşımıza çıkan özel şekillerden biri düzgün dört yüzlüdür. Bu yazıda düzgün dörtyüzlü ile ilgili bilmemiz gereken her şeye değineceğiz.
Öncelikle şunu belirtelim ki düzgün dörtyüzlü bir piramittir.
Yan yüzeyleri üçgen olan ve bir tepe noktasına sahip üç boyutlu geometrik şekillere piramit denir. Düzgün dörtyüzlü bir üçgen piramittir. Yani tabanı da üçgen olan bir piramittir.
Kimyada bazı molekül geometrileri düzgün dörtyüzlü ile modellenir. Bu nedenle bu geometrik yapıyı anlamak önemlidir. Konuyu anlamak için eğer bilmiyorsanız önce eşkenar üçgen konusuna çalışmalısınız.
Düzgün Dörtyüzlü Açılımı ve Özellikleri
Düzgün dörtyüzlünün kendine ait çeşitli özellikleri vardır. Ancak bu özellikleri bilmemiz için önce şekli ve açılımını anlamamız gerekir. Düzgün dörtyüzlünün 4 yüzeyi de 4 eşkenar üçgenden oluşmaktadır.
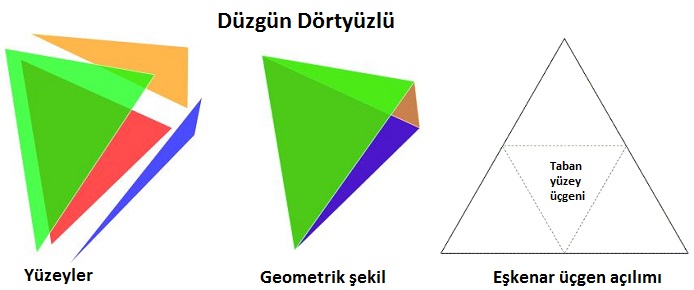
Yukarıdaki şekilde düzgün dörtyüzlü açılımı gösterilmiştir. Düzgün dörtyüzlünün özellikleri aşağıda sıralanmıştır.
- Düzgün dörtyüzlünün dört yüzü vardır, bunların hepsi eşkenar üçgenlerdir.
- Düzgün dörtyüzlüde, hepsinin uzunluğu eşit olan toplam 6 kenar vardır.
- Düzgün dörtyüzlünün dört köşesi vardır, herhangi bir köşede üç yüz birleşir.
- Düzgün dörtyüzlünün tüm yüzlerine teğet olan bir iç teğet küre vardır.
Düzgün Dörtyüzlü Formülleri
Düzgün dörtyüzlüde alan ve hacim bulmak için kullandığımız formüller vardır. Bu formülleri ezberlemekten çok mantığını anlamamız gerekir.
Düzgün dörtyüzlünün 4 yüzeyi olduğu için alanı 4 tane eşkenar üçgen alanı olacaktır. Bu üçgenler eş olduğu için formül şöyle olacaktır.
A = 4.a2.√3/4 = a2.√3 olur.
Tepe noktasından tabana indirilen dikme h olsun. h ile ayrıt uzunluğu olan a arasında şöyle bir bağıntı vardır.
h = a√6/3 olur.
Taban üçgeninde inen dikme L olsun. Bu dikme eşkenar üçgenin orta dikmesidir ve uzunluğu bu şekilde bulunur.
L = a√3/2 olur.
Piramitte hacim taban alanı x yükseklik / 3 şeklindedir.
Öyleyse a.h/3 düzgün dörtyüzlünün hacmi olacaktır. Bu durumda hacim:
V = a3√2/12 olacaktır.
Örnek Sorular
Aşağıdaki örnek sorularla konuyu pekiştirelim.
Soru: Bir düzgün dörtyüzlüde ayrıt uzunluğu a = 2√2 cm'dir. Buna göre cismin hacmi ne kadardır?
Çözüm: Hacim formülünü uygulamak için ayrıt uzunluğunun kübünü almak gerekir. Soruda a = 2√2 olduğuna göre a3 = 16√2 olur.
Formüle göre (V = a3√2/12) bu değeri √2 ile çarpıp 12'ye bölmemiz gerekir. Bu durumda cevap 32 / 12 = 8/3 cm3 olur.
Bir tane daha örnek çözelim ve konuyu kapatalım.
Soru: Bir düzgün dörtyüzlü şeklindeki bir cismin yüzey alanının 121√3 cm2 olduğu bilinmektedir. Buna göre bu cismin ayrıt uzunluğu kaç cm olur?
Çözüm: Alan hesabı için yukarıda formül vermiştik. Alan = a2.√3 olduğuna göre a2 = 121 buradan da a = 11 cm çıkar.
Etiketler:
Son Eklenenler
- Tarımla İlgili Meslekler
- Matematiği İyi Olmayanlar Hangi Mesleği Seçmeli?
- Antropoloji Nedir?
- Dünyanın Kaç Türlü Hareketi Vardır?
- Toplumsal Düzeni Sağlayan Kurallar Nelerdir?
- Cumhuriyet Yönetiminin Değerleri Nelerdir?
- İklim ve Hava Olayları Arasındaki Fark
- 1 Asal Sayı Mıdır?
- Homeostasi nedir?
- 2 ile Bölünebilme Kuralı
