Parabol Formülleri
Parabol matematiğin önemli konuları arasındadır. Bu yazıda konu içerisinde kullandığımız parabol formülleri üzerinde duracağız. Bu formüller aynı zamanda konunun genel iskeletini de oluşturmaktadır.
Parabolle ilgili daha geniş bilgiyi parabol konu anlatımı kısmında bulabilirsiniz.
Parabol Nedir?
Konu içerisinde anlattığımız gibi parabol ikinci dereceden denklem grafikleridir. İkinci dereceden bir denklemi koordinat sistemine aktarırsanız ortaya çıkan grafik bir parabol oluşturur.
İkinci dereceden denklemler y = ax2 + bx + c formunda olabilir.
Ayrıca parabol için özelleştirişmiş denklem de y = a.(x - r)2 + k şeklinde yazılabilir.
Bu iki denklem de aslında farklı yazılmış aynı denklemlerdir. İkisi de ikinci dereceden denklemdir.
Parabolde Tepe Noktası Formülleri
Tepe noktası parabolün anahtarıdır. Bu nedenle parabolde tepe noktasını bulmak çok önemlidir.
y = a.(x - r)2 + k şeklinde verilen bir denklem zaten tepe noktası üzerinden yazılmıştır. Bu nedenle tepe nokta T(r, k) olur.
Örneğin y = 2(x - 4)2 + 8 şeklinde verilen bir parabol denkleminde tepe noktası T(4, 8) noktasıdır.
Eğer denklem parabol formuna dönüştürülmeden doğrudan ikinci dereceden denklem şeklindeyse o zaman tepe noktasını bulmak için formülü uygulamamız gerekir.
Öreğin y = ax2 + bx + c formundaysa o zaman tepe noktasının apsisi –b/2a şeklinde bulunur. Bulunan nokta denklemde yerine yazılınca çıkan nokta tepe noktasının ordinatıdır.
Parabolün tepe noktasıyla ilgili bir örnek yaparak bütün bu anlattıklarımızın üzerinden geçelim.
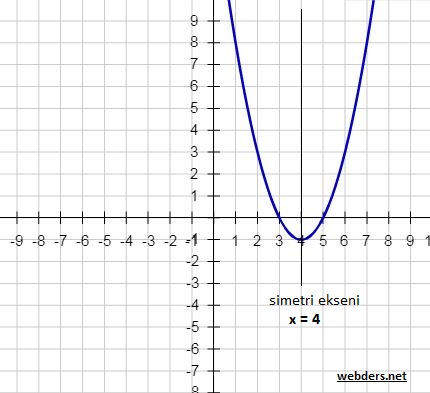
Örneğin y = x2 -8x + 15 denklemi verile parabolün tepe noktasını bulalım. Formülü yerine koymamız için b = -8, a = 1 olur. Bu durumda –b/2a = 4 olur. Yani parabolün tepe noktasının apsisi 4’tür. 4’ü yerine koyarsak denklemde 16 – 32 + 15 = -1 çıkar. Öyleyse tepe noktasının ordinatı da -1’dir. Yani tepe noktası T(4, -1) çıkar. Simetri ekseni de x = 4 doğrusudur. Çünkü tepe noktasının apsisi bu noktadır.
Şimdi bulduğumuz tepe noktası üzerinden parabol denklemini yeniden yazalım. Baş katsayı olan a = 1 olduğuna göre y = (x - 4)2 - 1 parabolün denklemi olur.
Kısaca toparlarsak y = x2 -8x + 15 = (x - 4)2 - 1 aynı anlama gelmektedir.
Bu parabolü çizersek aşağıdaki gibi bir görüntü elde ederiz.
Parabol Grafiği ile İlgili Formüller
Parabol grafiğini yorumlamak veya grafiğini çizmek için de kullandığımız birkaç önemli formül bulunmaktadır.
Önce delta ya da diskriminant (∆) kavramını öğrenelim.
y = ax2 + bx + c formundaki bir denklem için ∆ = b2 – 4ac şeklindedir. Bu durumda üç seçenek karşımıza çıkmaktadır.
- ∆ > 0 ise grafik x eksenini iki noktada keser. (iki farklı kökü vardır)
- ∆ = 0 ise grafik x eksenine teğettir. (çakışık iki kökü vardır.)
- ∆ < 0 ise grafik x eksenine değmez. (reel kök yoktur.)
Grafikle ilgili sorularda karşımıza çıkacak şeyler için bilmemiz gereken formüller ise şöyledir:
- a > 0 ise denklemin kolları yukarı doğrudur.
- a < 0 ise denklemin kolları aşağı doğrudur.
- c grafiğin y noktasında kestiği noktadır.
Bu formüller ışığında parabol grafiği çizme soruları kolaylıkla çözülebilir.
Bir parabolle ilgili karar verilmesi gereken şeyler şunlardır:
- Tepe noktası nerededir?
- Kollar yukarı mı aşağı mı yöndedir?
- Apsis (x) eksenini kesiyor mu?
- Ordinat (y) eksenini nerede kesiyor?
Bunlara cevap verildiği taktirde parabolün genel yapısı ortaya çıkacaktır.
Etiketler:
Son Eklenenler
- Tarımla İlgili Meslekler
- Matematiği İyi Olmayanlar Hangi Mesleği Seçmeli?
- Antropoloji Nedir?
- Dünyanın Kaç Türlü Hareketi Vardır?
- Toplumsal Düzeni Sağlayan Kurallar Nelerdir?
- Cumhuriyet Yönetiminin Değerleri Nelerdir?
- İklim ve Hava Olayları Arasındaki Fark
- 1 Asal Sayı Mıdır?
- Homeostasi nedir?
- 2 ile Bölünebilme Kuralı
