Enerjinin Korunumu

16.08.2017 - 08:39

Fizikte korunma terimi, değişmeyen bir şeyi ifade eder. Bir şeyin korunuyor olması denklemdeki değişkenin zaman içinde sabit olduğu anlamına gelir. Korunan şeyin olaydan önce ve sonra aynı değeri aynıdır.

Bu yazıda enerjinin korunumunu göreceğiz. Enerjinin korunumu yasası veya enerjinin korunumu kanunu şeklinde karşımıza çıkan bir fizik ilkesini irdeleyeceğiz.

Fizikte korunan birçok büyüklük vardır. Bu da karmaşık durumlarda basit tahminler yapmamızı son derece kolay hale getirmektedir. Mekanikte korunan üç temel büyüklük vardır:

Enerji
Momentum
Açısal momentum

Enerjinin Korunumu İçin Gereken Şartlar

Evde kullandığınız bir pilin enerjisi zamanla azalıp bitmektedir. Bu durumda enerjinin nasıl korunduğunu merak edebilirsiniz. Konuyu anlamak için eklememiz gereken birkaç önemli nokta bulunmaktadır. Bunlardan en önemlisi “enerji dönüşümü” olarak adlandırılan noktadır.

Fiziksel olaylarda enerji sürekli form değiştirip dönüşür.

Enerji, bu makalede tartışacağımız gibi, bir sistemin toplam enerjisine denilmektedir. Nesneler zamanla hareket ederken, onlarla ilişkili enerjiler örneğin kinetik, yerçekimi potansiyel enerjisi değişecektir. Ancak enerji korunursa, sistemdeki toplam aynı kalacaktır.

Enerjinin korunumu yalnızca izole edilmiş sistemler için geçerlidir. Kaba bir zemin üzerinde yuvarlanan bir top, enerji korunumu kanununa uymaz. Çünkü zeminle temas ederken enerjinin bir kısmını ona devredecektir.

Aslında zemin sürtünme yoluyla top üzerinde iş yapmaktadır. Bununla birlikte, topu ve zemini birlikte bir sistem olarak ele alırsak, o zaman enerjinin korunması gerçekleşecektir. Bu örnek üzerinden konunun anlaşılması daha kolaydır.

Birçok farklı alanda enerjinin korunumu geçerliyken biz basitleştirmek anlamında mekanik enerjiyi daha çok ele alacağız.

Mekanik Enerjinin Korunması

Mekanik enerji bir sistemdeki potansiyel enerjinin ve kinetik enerjinin toplamıdır.

E_M= E_P + E_K

Öyleyse yerden h kadar yükseklikle v kadar hızı olan bir cismin mekanik enerjisini şöyle ifade edebiliriz.

Potansiyel enerji = m.g.h
Kinetik enerji = ½.m.v²
Mekanik enerji = m.g.h + 1/2m.v²olur.

Bu cisim zamanla yere yaklaştığında v hızı artar. Aynı şekilde h yüksekliği de azalır.

Yani cismin potansiyel enerjisi azalırken kinetik enerjisi artar. Fakat mekanik enerji yine sabittir. Potansiyel enerjinin bir kısmı kinetik enerjiye dönüşmüştür. (Sistemde sürtünmenin olmadığı varsayılmaktadır.)

Sistem Derken Ne Kastediliyor?

Fizikte sistem, denklemlerimizle modellemeyi seçtiğimiz bir nesne topluluğuna verdiğimiz addır. Bir nesnenin enerjinin korunumu kullanılarak hareketi tanımlanacaksa, sistem nesneyi ve etkileşime girdiği diğer tüm nesneleri içermelidir.

Uygulamada, her zaman bazı etkileşimleri görmezden gelmeyi seçmek zorundayız. Bir sistemi tanımlarken, önem verdiğimiz şeyler etrafında bir çizgi çiziyoruz ve yapmadığımız şeyler. Dahil etmediğimiz şeyler genellikle topluca çevre olarak adlandırılır.

Ortamın bir kısmını göz ardı etmek kaçınılmaz olarak hesaplamamızı biraz bozacaktır. Bu hesaplamalardaki ihmaller olayı daha basit hale getirip anlamak içindir. Yoksa gerçek bir fiziksel olayı hesaplarken ortamda bulunan diğer etkileri de hesaba katarak doğruya en yakın sonucu elde edebiliriz.

Kendi Enerjisini Üreten Makineler Neden Üretilemez?

Sistem ve enerji korunumu kavramlarını anladıysak bu soruya rahatlıkla cevap verebiliriz. Makine kapalı sisteminin çalışırken kaybettiği enerji vardır. Sonsuza kadar çalışıp kendi enerjisini üretmesi için enerji veriminin %100 olması gerekir. Bu da kayıptan dolayı mümkün değildir.

Bilimsel birçok kuruluş kendilerine birçok kendi enerjisini üretip devamlı çalışabilen makine projelerini getirdiklerini ifade ediyor. Bu projeler termodinamiğin temel yasalarına uymadıkları için doğrudan reddediliyor. Çünkü enerji kaybı buna müsaade etmiyor.

Enerjinin korunumu deneylerinde de bir kısım enerjinin ortama aktarıldığı görülür.

Enerjinin Korunumu ile İlgili Örnekler

Enerji korunumunun ne olduğundan bahsettik. Şimdi konuyla ilgili örnekler verip soru çözerek konu anlatımımızı tamamlayalım.

Örnek: 10 metre yüksekte duran 2 kg kütleli cisim serbest bırakılmaktadır. Cisim 5 metre yüksekliğine geldiğinde hızı ne olur? (g = 10)

Çözüm: Atışlar konusunu bilen arkadaşlar için bu soru oldukça kolay bir sorudur. Ancak konuyu bilmeseniz dahi enerjinin korunumuyla bu soruyu rahatlıkla çözebilirsiniz.

İlk durumda cisim durduğu için hızı v = 0 olur. Öyleyse kinetik enerjisi de 0’dır. 10 metre yükseklikle olduğuna göre potansiyel enerji E_P = m.g.h = 2.10.10 = 200 olur.

Cisim 5 metre yüksekliğine indiğinde potansiyel enerjisi E_p = 2.10.5 = 100 olacaktır.

Demek ki geriye kalan enerji kinetik enerjiye dönüşmüştür. İlk durumda 0 olan kinetik enerji 100 olmuştur.

Öyleyse E_k = ½.m.v² = 100 olacaktır. Ek = ½.2.v² = 100, v² = 100, v = 10 m/s bulunur.

Bir de resimli örnek çözelim.

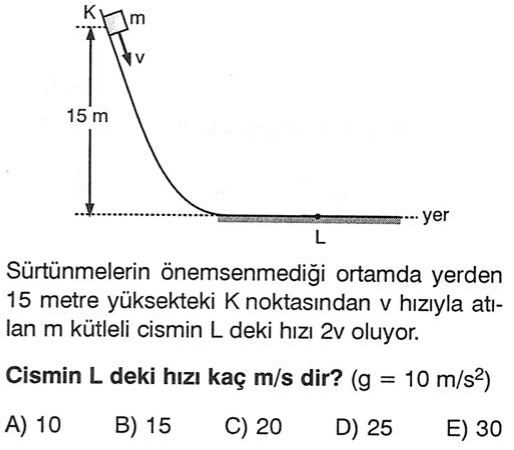
Çözüm: Sistemde sürtünme yok ve dışarıdan da herhangi bir müdahale olmuyor. Öyleyse enerji korunur.

Cismin ilk durumda K noktasındayken hızı v ikinci durumda L noktasında ise 2v olmuştur. İki durumda da mekanik enerji eşittir. Bize L noktasındaki 2v hızını sormaktadır.

Birinci durumda

Mekanik = potansiyel + kinetik = 15.10.m + ½.m.v² = 150m + ½.mv2 olur.

İkinci durumda

Yükseklik olmadığı için potansiyel enerji sıfırlanmıştır.

Mekanik = 15.0.m + ½.m(2v)² = 0 + ½.m.4v² olur.

İki durumu eşitlersek 150m + ½.mv² = m2v² eşitliği elde edilir.

Eşitlikte m’ler ortak olduğu için eleyebiliriz. Bu durumda 3/2.v² = 150, v² = 100, v = 10 m/s olur.

Hemen 10 olan şıkkı işaretlemeyin. Soruda bize L’deki hızı yani 2v’yi sormaktadır. Öyleyse yanıt 20 yani C seneği olur.

Etiketler:

fizik

Yorumlar

Yorum Yap