Katılarda ve Canlılarda Dayanıklılık

10.08.2017 - 13:11

Dayanıklılık maddenin özelliklerinden bir tanesidir. Katılarda dayanıklılık fizik müfredatı içerisinde 9. Sınıf konusu olarak girmiştir.

Katıların dayanaklılığı ve daha özelinde canlıların dayanıklılığını bu derste öğreneceğiz. Dayanıklılık için bilmemiz gereken formülleri de konu içerisinde elde edeceğiz. Şimdi dayanıklılık nedir sorusuyla konuya başlayalım.

Dayanıklılık Nedir?

Bilindiği gibi katı halde maddenin atomları arasındaki boşluk en azdır. Bu boşluklar gözle görülemez. Dolayısı ile katı maddeye baktığımızda boşluk yokmuş gibi algılarız.

Katı bir maddenin kütlesi, hacmi ve şekli belirlidir.

Katı maddelerin şekil değiştirebilmeleri için dışardan bir kuvvet uygulanması gerekir. Dışardan bir kuvvet uygulanmadıkça hacimleri değişmez. Peki, bu kuvveti artırırsak ne olur? Belki bir kalem kaybınız olacak ama bunu deneyerek görebilirsiniz. Elinizdeki kaleme bir kuvvet uyguladığınızda eğilme ya da bükülme gözlenebilir. Kaleminiz kırılmaya karşı bir direnç gösterecektir. Bu direnç maddelerin dayanıklılığı olarak bilinir.

Cisimlerin üzerlerine uygulanan kuvvete karşı göstermiş oldukları dirence dayanıklılık denir.

Uygulanan kuvvet dayanıklılıktan küçük ise cismin şeklinde kalıcı ya da geçici birtakım değişiklikler olur. Kaleme uygulanan kuvvet dayanıklılıktan küçükse kalem esner, büyük ise kırılır. Tahta bir kalemi kırmak için uyguladığımız kuvvet ile demir bir kalemi kırmak için uyguladığımız kuvvet aynı değildir. Bu bize dayanıklılığın maddeden maddeye değiştiğini gösterir.

Dayanıklılık, maddeler için ayırt edici bir özelliktir.

Katılarda Dayanıklılık

Tarif ettiğimiz üzere dayanıklılık genellikle katılar söz konusu olduğunda karşımıza çıkar. Canlılarda dayanıklılığı ele alırken de aslında yine aynı mantığı kullanırız.

Dayanıklılık, maddenin kesit alanına da bağlıdır. İnce bir odun parçasını elimizle çok rahat kırabildiğimiz halde kalın bir kalası elimizle kıramayız. Yüzey alan arttığında dayanıklılık da artar. Dayanıklılığın kalınlığa bağlı değişimi,

Dayanıklılık = k.(kalınlık)² eşitliği ile ifade edilir.

Şekildeki r yarıçaplı K telinin dayanıklılığı 1 birim ise, 2r yarıçaplı L telinin dayanıklılığı 4 birimdir. Dayanıklılık, mukavemet olarak da bilinir.

Mukavemet, yük etkisi altında cisimlerin gerilme ve şekil değiştirme durumlarının incelendiği uygulamalı mekaniğin bir dalıdır.

Dayanıklılık birçok mühendislik dalının da temel konularındandır. Özellikle:

İnşaat
Makine
Gemi inşaatı
Uçak mühendisliği

Gibi alanlarda yaygın olarak kullanılır.

Bir bina kolonunun, uçak kanadının veya makine dişlisinin maruz kalacağı herhangi bir kuvvete dayanabilecek şekilde tasarlanması çok önemlidir. Dayanıklılık genel olarak;

Gerilme
Burulma
Kırılma
Basit eğilim
Enine yükleme
Gerilme ve şekil değiştirme
Kiriş ve mil tasarımı
Kolon ve kolon tasarımı

Gibi birçok konuyu inceler.

Dayanıklılıkta temel amaç; cisimlerin yük taşıma kapasitelerinin dayanım, rijitlik ve stabilite bakımından araştırılmasıdır. Bir cismin dayanıklılığı aşağıdaki niceliklere bağlıdır:

Şekil
Boyut
Kuvvetin uygulama hızı
Cismin yapıldığı maddenin cinsi
Sıcaklık

Canlılarda Dayanıklılık

Bir insan kendi ağırlığının 0,86 katını kaldırabilirken atlar yalnızca kendi ağırlıklarının yarısı kadarını kaldırabilirler. Ancak Leaf Beetle (Donacia) adlı böcek kendi ağırlığının 42,7 katı kadarını kaldırabilirken karıncalar kendi ağırlıklarının 52 katını kaldırabilmektedirler.

Bu nedenle arınca dayanıklılığı diye bir kavram oluşmuştur.

İnsanları yük kaldırma bakımından karınca ile kıyaslayabilmemiz için bir insanın 4500 kg’lık (4,5 tonluk) ağırlığı kaldırabilmesi gerekir. Dünyanın en iyi haltercisi olarak gösterilen Naim Süleymanoğlu, en fazla kendi ağırlığının 3 katını kaldırabilmiştir.

Vücutlarının 200 katı uzunluğundaki bir mesafeye kadar zıplayabilen pireleri kendimizle kıyasladığımızda bizim 70 katlı bir binaya zıplayabilmemiz gerekir. Pireler kadar yetenekli olmasalar da bazı böcekler de vücutlarının 80 katı kadar uzağa zıplayabilmektedir.

Hamam böcekleri vücutlarının 50 katı uzunluğundaki bir mesafeyi birkaç saniyede koşabilirler. Bu yaklaşık 30 cm demektir.

Bir koşucunun hamam böceği ile yarışabilmesi için saniyede 91 metre koşması gerekir. Atletizmde en hızlı koşucunun 100 m mesafeyi 9,69 saniyede koştuğunu düşünürsek aradaki farkı daha iyi anlarız. Bu ve benzeri örnekleri çoğaltabiliriz. Canlılar alemi birbirinden çok farklı sanatlar ve mimari harikalarla doludur. Her bir canlı farklı ölçeklerde yaratılmıştır. Bir kediyi vücuduna ait tüm oranları koruyarak bir fil kadar büyük veya bir pire kadar küçük hâle getirebilseydik nasıl bir görüntüyle karşılaşırdık acaba? Bu durumda kediler mevcut olan yeteneklerini ve özelliklerini koruyabilirler miydi dersiniz?

Büyüme ile ilgili olan genleri kontrol edip üzerlerinde oynama şansımız olsaydı filmini seyrettiğimiz dev goril King Kong gerçek olabilir miydi sizce? Bu tür soruların cevabını mantık yürüterek ve boyut analizi yaparak bulabiliriz:

Dayanıklılık Formülleri

Küp ve küre üzerinden dayanıklılık formülümü elde etmeye çalışalım.

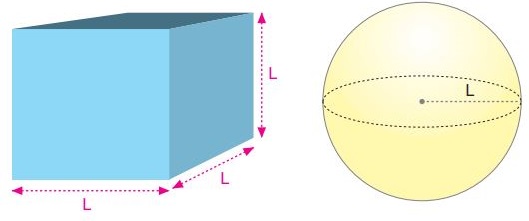
Küpün hacmi V = L³, yüzey alanı A = 6L², yüzey alanının hacme oranı ise,

A/V = 6L²/L³ = 6/L olur.

Benzer şekilde kürenin hacmi, V = 4/3.π.L³, yüzey alanı A = 4πL², yüzey alanın hacme oranı ise,

A/V = 4πL²/4/3.π.L³ = 3/L bulunur.

Bu iki örnekte de gördüğümüz gibi herhangi bir üç boyutlu cisim için karakteristik uzunluk L ise alanı L² ile hacmi de L³ ile orantılıdır. Alanın hacme oranı ise 1/L’dir.

Bu bize yüzey alanın hacme oranının büyük canlılarda küçük, küçük canlılarda büyük olduğunu gösterir.

Dikkat ederseniz canlılarda dayanıklılık yüzey alanı hacim ilişkisi ile ilgilidir.

Fil ve Karınca Örneği

Bir filin kulaklarının neden o kadar büyük olduğunu hiç merak ettiniz mi? Canlılarda ısı üretimi hacimleri ile orantılıdır. Isının dış ortama verilmesi canlıların yüzey alanlarına bağlıdır. Eğer filin kulakları o kadar büyük olmasaydı ürettiği fazla ısıyı dış ortama aktaramazdı. Yani kendi ısısı ile pişerdi.

Filin dayanıklılığı karıncanın dayanıklılığı ile kıyaslandığında oldukça küçüktür. Çünkü yüzey alanı/hacim oranı çok düşüktür.

Küçük canlılarda ısı kaybı çok olduğu için bu canlıların metabolizmalarının çok hızlı çalışması gerekir. Farenin metabolizma hızı filinkine göre çok çok büyüktür. Bu da tükettiği besinlerin miktarına yansır. Fareler vücut ağırlıklarının % 25 ile % 50’si kadar yerken minik bir kuş olan arı kuşu, ağırlığından daha fazla yem yemek zorundadır.

9. sınıfta gördüğümüz gibi güç birim zamanda yapılan iştir. Kısaca gücü, kuvvet ile hızın çarpımı olarak da düşünebiliriz. Her bir hayvanın harcadığı güç (metabolik hızları), yüzey alanı veya L² ile orantılıdır. Yani kaslara oksijen sağlanması birim zamanda kas hücrelerine gelen oksijenle ilgilidir.

Benzer bir mantık yürütme canlıların dayanıklılığı hususunda yapılabilir. Ayakları üzerinde yürüyen bir canlıyı ele alırsak vücut ağırlığını destekleyen bacaklar bir çubuk olarak düşünülebilir. Bacakların dayanıklılığı kesit alanları ile orantılı iken ağırlığı hacmi olan L³ ile orantılıdır. Başka bir ifadeyle dayanıklılık 1/L ile orantılıdır.

Canlının karakteristik uzunluğu (L) arttıkça dayanıklılık oranı azalacaktır yani aynı dayanıklılığı sağlamak için normalden daha kalın bacak kemiklerine ve daha fazla kasa ihtiyaç duyacaktır . Bu nedenle bir fareyi, orantılı şekilde filin büyüklüğüne ulaştırmış olsanız bile bu garip canlı muhtemelen yetersiz kaslardan dolayı hareket edemeyecek veya hareket sırasında bacakları kırılacaktır. Fil ve Brachiosaurus dinozoru gibi dev canlıların vücutları ile orantısız kalın bacakları, canlılarda tesadüfe yer olmadığını açıkça göstermektedir. Bu durumda dev goril, dev arılar veya böcekler gibi kurgu filmler her zaman bir fantezi olarak kalacaktır.

Dayanıklılıktan bahsetmişken bir kediyi 10 katlı bir binadan attığımızda fazla zarar görmez ama aynı durum bir insan veya fil için ölümcül sonuçlar doğurabilir.

Bir bebeğin tüm organlarını aynı oranda büyüterek yetişkin bir insan oluşturamayız. Çünkü bebek doğduğunda kafasının büyüklüğünün vücut büyüklüğüne oranı yetişkinlere göre daha fazladır. Ayrıca bebekte burun ucu, yukarıdan aşağı doğru yüzün tam ortasında yer alır. Yetişkinlerde ise burun ucu yukarıdan aşağı doğru yüzün sinde yer almaktadır. İnsan, yetişkinliğe ulaştığında gözleri iki kat büyürken kolları dört kat büyür.

Canlılardaki büyüme oranları, insan eliyle yapılmış mühendislik tasarımlarında olduğu gibi sabit olmayıp büyümenin her safhasında değişim gösteren dinamik bir süreçtir .

normal hacmi V_o = πr²h

normal kütle m_o = V_o.d

büyütülmüş hacim V = π(2r)².2h = 8V_o

büyütülmüş kütle m = V.d = 8V_o.d = 8m_o olur.

Yani canlıların boyutlarını iki katına çıkarırsak kütleleri dolayısı ile ağırlıkları 8 kat artar. Dayanıklılık r² ile orantılı olduğundan yarıçap 2 katına çıkarsa dayanıklılık 4 katına çıkar. Ama ağırlık 8 katına çıktığından bağıl olarak ağırlığımızdaki artış iki kat olur. Bunu daha iyi anlayabilmeniz için kilonuzun şimdiki değerinin iki katına çıktığını düşünmeniz yeterlidir. Bu durumda iki saat bile yürüyemez, yere yığılırsınız.

Etiketler:

fizik

Yorumlar

Yorum Yap