Doğru Denklemi

20.07.2017 - 06:51

Bu yazıda doğru denklemi ile ilgili bilmeniz gereken her şeyi öğreneceksiniz. Böylece doğru denklemleriyle ilgili aklınızda herhangi bir soru işareti kalmayacaktır.

Yazıda öğreneceğiniz temel konular şunlardır:

Bir noktası bilinen doğru denklemi
Eksenleri kestiği noktaları bilinen doğrunun denklemi
İki noktası bilinen doğrunun denklemi
y = mx + n türündeki doğrular

Her koşulda doğru denklemini rahatlıkla ortaya çıkarmak ve işlem yapmak istiyorsanız kolaycılığa kaçmayın ve konuyu iyi öğrenmeye çalışın. Zor olmadığını kendiniz de fark edeceksiniz.

Eğimle Konuya Başlayalım

Doğru denince aklımıza ilk gelmesi gereken şey eğimdir. Her doğrunun bir eğimi vardır. Eğimi bilinen bir doğrunun hangi doğrultuda uzandığı bilinebilir.

Eğim kısaca sarplık demektir. Bir dağ ne kadar sarp ve tırmanması güçse o dağ o kadar yüksek eğimlidir. Aşağıdaki doğru parçalarının eğimini bakın. Sizce hangisinin eğimi daha yüksek?

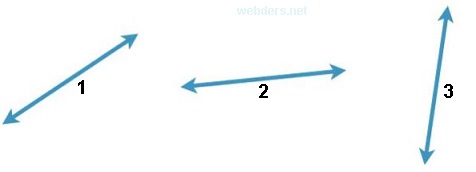
Doğru bildiniz. 3 numaralı doğru daha dik bu nedenle eğimi daha yüksektir. Eğim işte bu denli basit bir şeydir. Şimdi de eğimi matematiksel olarak ifade edelim.

Eğim matematikte m harfi ile gösterilir. Bu da doğrunun düşeyde aldığı yolun yatayda aldığı yola olan oranıdır. Resimde gördüğümüz 3 numaralı doğru yatayda az ilerlediği taktirde düşeyde epey yükselmiştir. Bu nedenle eğimi yüksektir.

Resimde bir doğru parçasının eğimi hesaplanmıştır. Görüldüğü gibi doğru parçasının yatayda aldığı mesafe düşeyde aldığı mesafeden az olduğu için eğimi 1'den küçüktür.

Koordinat sisteminde eğim gösterilirken noktaların arasındaki mesafe temel alınarak gösterilir.

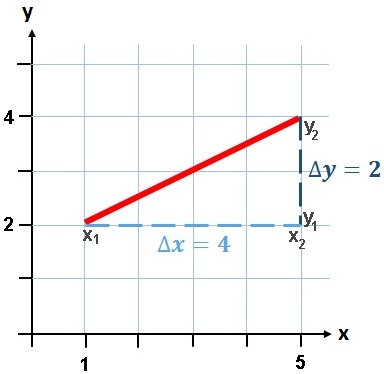
Yukarıdaki resme göre eğim formülü m = Δy / Δx şeklinde gösterilebilir. Bu da aynı zamanda m = (y₂ - y₁) / (x₂ - x₁) demektir. (Eğimin tek olayı y'ler farkını x'ler farkına bölmektir.)

Eğimin genel mantığı anlaşıldığına göre şimdi doğru denklemlerine geçebiliriz.

Bir Noktası Bilinen Doğru Denklemi

Doğru üzerinden bir noktayı bilmek o doğrunun denklemini yazmak için yeterli olmayacaktır. Çünkü bir noktadan sonsuz tane doğru geçer. Bu nedenle bir noktası bilinen doğru denklemi yerine "eğimi ve bir noktası bilinen doğru denklemi" demek daha doğru olacaktır.

Şimdi eğim üzerinde neden durduğumuzu anladınız mı? Eğimi bildiğimiz taktirde bir nokta üzerinden doğrunun denklemini çıkarabiliyoruz.

Aslında bir nokta üzerinden sonsuz doğru geçtiği için eğimini bildiğimiz zaman o nokta üzerinden geçen "falan" eğimli doğru diye tanımlamış oluyoruz. Böylece doğruyla ilgili bütün bilgiler elimize geçiyor.

Eğimi ve bir noktası bilinen doğru denklemi yazılırken şu adımlar takip edilir:

Eğimi formülünü yaz.
Formülde y₂ve x₂ yerine y ve x yaz.
Formülde y₁ ve x₁yerine bildiğin noktayı yaz.
İçler dışlar çarpıp denklemi elde et.
Bilinen ve bilinmeyenleri bir tarafa toplayıp denklemi elde et.

Bu adımları takip ettiğimiz zaman doğrunun denklemini rahatlıkla yazabiliriz. Şimdi bir örnekle durumu pekiştirelim.

Örnek: Eğimi 3 olan ve (2, 5) noktasından geçen doğrunun denklemini yazısınız.

Çözüm: Yukarıda yazdığımız adımları aynen uyguluyoruz.

3 = (y₂ - y₁) / (x₂ - x₁)

3 = (y - y₁) / ( x - x₁) (ikinci adımı uyguladık.)

3 = (y - 5) / (x - 2) (bilinen noktayı yerine yazdık.)

3.(x - 2) = (y -5) (içler dışlar çarptık)

3x - 6 = y -5 (denklemi açtık)

3x - y -1 = 0 (denklemi 0'a eşitleyip elde ettik.)

Görüldüğü gibi denklemi elde etmek çok kolay.

Bu tür örneklerde denklemi elde etmek için eğimini bir daha test edin.

Denklemi verilmiş bir doğrunun eğimi m = -a/b ile bulunur. Burada a x'in katsayısı, b ise y'nin katsayısıdır.

Görüldüğü gibi m = -3 / -1 = 3 çıkacaktır. (Denklem eğimi sağlıyor.)

Bir örnek daha yapalım.

Örnek: Koordinat sisteminde (2, 1) noktasından geçen ve eğimi 2 olan doğrunun denklemini yazınız.

Çözüm: Artık pratiktik kazandıysak doğrudan şunu yazmamız gerekir:

2 = (y - 1) / (x -2) (Bunu rahatlıkla yazabiliyor olmamız gerekir.)

2.(x - 2) = (y - 1)

2x - 4 = y - 1

2x - y - 3 = 0 (Denklem kolaylıkla çıktı.)

Eksenleri Kestiği Noktaları Bilinen Doğrunun Denklemi

Yukarıda konu üzerinde dururken şunu belirttik. Bir doğru denkleminin yazılması için doğruya ait en az bir nokta ve doğrunun eğimi bilinmelidir diye. Burada da durum aynen geçerlidir.

Eksenleri kestiği noktaları bilinin doğrunun denklemi yazılırken yine eğim ve bir nokta bulunur. Eğimi eksenleri kesen noktalardan bulabiliriz. Nokta için de zaten eksenleri kesen herhangi bir noktayı kullansak yeterli olur.

Yukarıda anlatılanları özümsediysek burada hiç zorlanmayacağız. Bir örnekle işe başlayalım.

Soru: Koordinat sisteminde y ekseninin 3 ordinatında ve x eksenini -3 apsisinde kesen doğrunun denklemini yazısınız.

Çözüm: Sorunun çözümünde hemen aklımız eğime gitmelidir. Doğrunun eğimini nasıl elde edebiliriz?

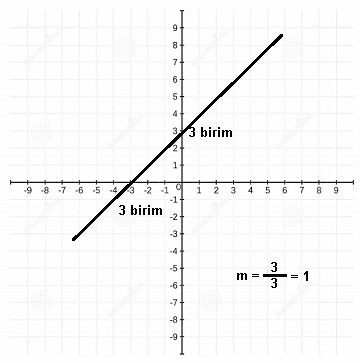
Yukarıdaki resimde bahsettiğimiz doğrunun çizilmiş şekli bulunmaktadır. Görüldüğü gibi x eksenini -3 ve y eksenini 3 noktasında kesmiştir. Eğimi ise 1 birim olmuştur.

Burada dikkat edilmesi gereken eksenleri kesen noktaların (-3, 0) ve (0, 3) noktaları olduğudur. Bir eksene değdiği zaman diğer eksenin değeri 0 olacaktır.

Şimdi eğimi biliyoruz. Elimizde de iki nokta var. Denklemi yazmak için rastgele bir noktayı seçelim. Negatif işaretle uğraşmamak için (0, 3) noktasını seçelim.

1 = (y -3) / (x - 0)

x - 0 = y - 3

x - y + 3 = 0 (Denklemi elde ettik.)

İki Noktası Bilinen Bir Doğrunun Denklemi

Burada da temel mantığımız aynı olacaktır. Bir nokta ve eğime ihtiyacımız var. Nokta olarak verilen iki noktadan rastgele birini kullanabiliriz. Yine bulmamız gereken eğim olmaktadır.

İki noktası bilinen bir doğrunun denklemini yazarken eğimi bulmak için noktaların arasındaki farkı alıp oranlarız. Hangi noktayı önce yazdığımızın bir önemi yok. Önemli olan y'lerden y'leri, x'lerden de x'leri çıkarmaktır.

Yukarıda eğim formülünü verirken m = (y₂ - y₁) / (x₂ - x₁) ifadesini vermiştik zaten.

Örneğin (3, 5) ve (6 , 12) noktalarından geçen doğrunun eğimini bulalım.

Yapacağımız çok basit bir işlemdir. 12 - 5 = 7, 6 / 3 = 2 öyleyse eğim m = 7/2 olur.

Problem: Koordinat düzleminde (4, -1) noktasından ve (8, 5) noktalarından geçen doğrunun denklemini yazınız.

Çözüm: En başından beri farklı bir şey yapmadık. Eğim ve bir noktayı denklem için kullandık. Burada da elimizde iki nokta bulunmakta ancak eğimi hesaplamamız gerekiyor.

m = (5 - (-1)) / (8 - 4) = 6 / 4 = 3/2 olur.

Şimdi de denklemi yazmak için (8, 5) noktasını seçelim. (Ben içinde - olmayan noktayı seçiyorum genellikle)

3/2 = (y - 5) / (x - 8)

3x - 24 = 2y - 10

3x - 2y - 14 = 0 olarak bulunur.

İsterseniz eğim testine tabi tutabilirsiniz. Ya da denklemi bulduktan sonra herhangi bir noktayı yerine koyup deneyebilirsiniz.

Unutmayın bir denklem doğruysa üzerindeki bütün noktaları sağlamak zorundadır.

Demin (8, 5) noktasını yerine koyarak denklemi elde ettik. Peki, diğer noktayı denkleme yazarsak denklemi sağlar mı?

Elbette sağlamak zorundadır. Sağlamıyorsa denklemi yanlış kurmuşuz demektir. Sağlamasını yapmak için diğer noktayı yani (4 - 1) noktasını yerine yazalım.

3.4 - 2(-1) - 14 = 0

12 - (-2) - 14 = 0

0 = 0 (denklemi diğer nokta da sağlıyor.)

Farklı Formattaki Doğru Denklemleri (y = mx + n)

Şimdiye kadar denklemlerin sağ tarafını 0'a eşitleyerek denklem kurduk. Ancak bazı örneklerde denklemle y yalnız bırakılır.

Yani denklem y = mx + n formatına getirilir. Burada farklı bir şey yoktur. Denklemde y'yi yalnız bırakarak siz de kolaylıkla bu tür bir denklem elde edebilirsiniz.

Örneğin yukarıdaki problemde elimizde olan denklemi bu formata dönüştürelim. Bunun için y'yi bir tarafta diğerlerini ise diğer tarafta toplamamız gerekir.

3x - 2y - 14 = 0

2y = 3x - 14

y = (3/2)x - 7 olarak elde edilir.

Bu tür denklemlerde y yalnız bırakıldığında x'in katsayısı eğim olur. (Eğimi 3/2 bulmuştuk zaten)

Bu nedenle y = mx + n şeklinde bu doğrular genelleştirilmiştir.

Doğru denklemleri ile ilgili ihtiyacımız olan en temel bilgileri detaylı ve basit bir şekilde anlatmaya çalıştık. Konunun pekişmesi için bol miktarda örnek soru çözmeyi ihmal etmeyin.

Etiketler:

matematik

geometri

Yorumlar

Yorum Yap