Simetrik İki Kök
Denklem kökleriyle ilgili olarak “simetrik iki kök” kavramı karşımıza çok çıkmaktadır. Simetrik iki kökün ne olduğunu bilirsek soruları daha doğru yorumlarız. Soruda bize simetrik iki kökle verilmek istenen bir bilgi vardır. Öncelikle denklemde kök ne demektir ona değinelim. Yazıyı sonuna kadar okursanız çok önemli bir şeyi öğrenmiş olacaksınız.
Denklemin Kökü
Bir denklemin kökü o denklemi sağlayan değerdir. Denklem çözerken denklemin bir tarafı genellikle 0’a eşitlenir. Denklem kaçıncı derecedense denklemin o kadar kökü vardır. Bu kökler reel sayılarda ya da karmaşık sayılarda olabilir.
Birinci derecede denklemde bir kök vardır:
Örneğin x + 2 = 9 denklemini çözmek için bir tarafı 0’a eşitleyelim. 9’u sol tarafa – işaretiyle atarsak x – 7 = 0 denklemini elde ederiz. Buradan da x = 7 çıkar. 7 bu denklemin tek köküdür.
Denklem ikinci dereceden olursa bu sefer kök sayısı ikiye çıkar.
(x- 2).(x+3) = 0 ifadesinde ikinci dereceden bir denklem vardır. Bu denklemi 2 ve -3 değerleri 0’a eşitler. Bu değerler bu denklemin köküdür. Denklemi açarsak içerisinde x2’li ifade olduğunu görebiliriz. Bu da denklemin ikinci dereceden olduğunu gösterir.
(x- 2).(x+3) = x2 + x – 6 = 0
Denkleminin simetrik iki kökü vardır diyorsa bu denklemin ikinci dereceden olması gerekir. Demek ki simetrik iki kök kavramı ikinci derece denklemler için geçerlidir.
Grafikte Denklem Kökleri
İkinci dereceden denklemin kökleri onları sıfır yapan noktalardır dedik. Bu durum grafikte y’nin 0 olduğu yani eğrinin x eksenini kestiği durumlarda mümkündür. Demek ki bir grafikte denklemin kökleri x eksenini kesen noktalardır.
Aşağıdaki grafik ikinci derecen bir denklemin grafiğidir. Grafiğe bakarak denklem köklerinin -1 ve -3 olduğunu rahatlıkla anlayabiliriz.
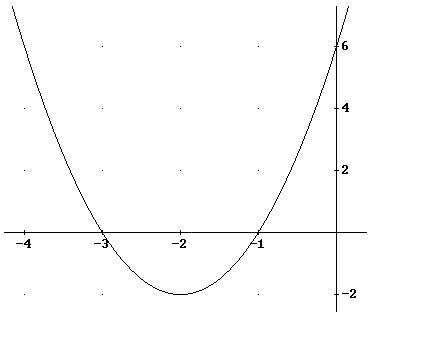
Simetrik iki kök olduğu zaman grafiğin x eksenine değen iki noktanın y eksenine göre simetrik olması gerekir. Bu da köklerin zıt işaretli olması demektir. Yani bir kök 2 ise diğer kök -2 olur. Bir kök 3 ise diğer kök -3 olur.
Aşağıdaki denklemin kökleri 1 ve -1’dir. Denklemin simetrik iki kökü vardır. Dolayısıyla grafikten de bu simetrik görülmektedir.
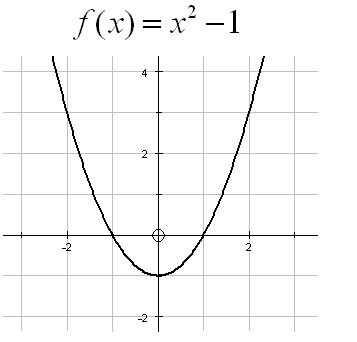
Buradan şöyle bir sonucu çıkarabiliriz. Eğer kökler zıt işaretliyse o zaman kökler toplamı 0 olur. İkinci dereceden denklemlerde kökler toplamı –b/a formülü ile bulunur. Bu formülün 0’a eşit olması için de b’nin 0 olması gerekir.
Sonuç olarak simetrik iki kök varsa kökler toplamının 0 olması gerekmektedir. Bu da (x-3).(x+3) = 0 gibi denklemlerde mümkündür. Aşağıdaki denklemlerin simetrik iki kökü bulunmaktadır.
- X2 – 4 = 0
- X2 – 9 = 0
- X2 – 16 = 0
Etiketler:
Son Eklenenler
- Tarımla İlgili Meslekler
- Matematiği İyi Olmayanlar Hangi Mesleği Seçmeli?
- Antropoloji Nedir?
- Dünyanın Kaç Türlü Hareketi Vardır?
- Toplumsal Düzeni Sağlayan Kurallar Nelerdir?
- Cumhuriyet Yönetiminin Değerleri Nelerdir?
- İklim ve Hava Olayları Arasındaki Fark
- 1 Asal Sayı Mıdır?
- Homeostasi nedir?
- 2 ile Bölünebilme Kuralı
