Eğim Formülü
Eğim matematikte ve geometride önemli bir kavramdır. Eğim bir doğrunun yataylık - diklik oranını bize veren bir bilgidir. Yani iki boyutlu düzlemde x ve y düzlemlerini kaplama oranlarını bize söyler. Eğim için m ifadesi sembol olarak kullanılır.
Bir doğrunun eğimini hesaplamak için o doğru üzerinde, herhangi iki noktayı bilmek yeterlidir. Bu noktalar arasında y düzlemindeki değişimi, x düzlemindeki değişime oranlarsak eğimi elde ederiz. Yani eğimin formülü şöyledir: 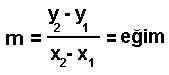
İfadelerin numaralandırılması kafa karışıklığına yol açabilir. Aslında y2 ve y1 aynı doğru üzerindeki rastgele iki ordinat noktası demektir. Aynı şekilde x2 ve x1 de apsis ekseni üzerindeki iki noktadır.
Örnek: (3, 5) ve (8, 12) noktalarından geçen doğrunun eğimini bulalım.
Burada yapmamız gereken tek şey y değerlerinin farkını, x değerlerinin farkına bölmektir. Yani m = (12 - 5) / (8 - 3) = 7/5 olur.
Eğim Formülünün Sonuçları
Eğim formülü eğimi bulmamıza yarayan bir kolay yoldur. Eğimin matematikte birçok anlamı vardır. Öncelikle eğim apsisle yapılan pozitif yönlü açının tanjantı demektir. Aynı zamanda eğim birinci dereceden türevdir. Bu bilgileri kullanarak doğrunun eğiminden farklı bilgilere ulaşabiliriz. Eğim formülünün bize sağladığı bazı sonuçlar şöyledir:
- Eğer formülde çıkan sonuç pozitifse, doğru yukarı yönlü devam ediyor demektir.
- Eğer formülde değer negatif çıkarsa, doğru aşağı yönlüdür.
- Yatay doğruların eğimi 0'dır. Çünkü y'ler farkı sıfır olacaktır.
- Düşey doğruların eğimi tanımsızdır. Çünkü paydada olan x'ler farkı 0 olacaktır. Paydada 0 olması kesri tanımsız yapar.
- Paralel doğruların eğimi eşittir. Bu nedenle doğrularda paralellik varsa birinin eğimini diğeri için kullanabiliriz.
- Dik doğruların eğimlerinin çarpımı -1'dir.
Yukarıdaki bilgiler eğimle alakalı, hayatımızı kurtaracak bilgilerdir. Bu bilgileri kullanarak matematikte doğru denklemlerini ve doğrunun analitiğini daha kolay kavrayabiliriz. Eğim kavramı matematiğin temel kavramlarından biridir.
Eğim Açısı
Eğim için tanjant kullanarak da hesaplama yapabiliriz. Örneğin y = x doğrusunun eğimi 1'dir. Çünkü y'deki her değişim için x de eşit olarak değişecektir. Bunun sonucunda y = x doğrusu apsis ekseniyle 45 derecelik açı yapar. Çünkü tan45 = 1 eşitliği vardır. Burada karıştırılmaması gereken açının pozitif yönlü olarak alınmasıdır.
Eğim açısı doğrunun sağ-üst tarafında kalan açıdır. Bu açı x ekseniyle yapılır. Eğim açısının tanjantı eğimi verir.
Etiketler:
Son Eklenenler
- Tarımla İlgili Meslekler
- Matematiği İyi Olmayanlar Hangi Mesleği Seçmeli?
- Antropoloji Nedir?
- Dünyanın Kaç Türlü Hareketi Vardır?
- Toplumsal Düzeni Sağlayan Kurallar Nelerdir?
- Cumhuriyet Yönetiminin Değerleri Nelerdir?
- İklim ve Hava Olayları Arasındaki Fark
- 1 Asal Sayı Mıdır?
- Homeostasi nedir?
- 2 ile Bölünebilme Kuralı
