Üçgenin Çevresi
Üçgenin çevresi hesaplamak açısından çok kolay olmasına rağmen birçok öğrenci bilmediği için işlem yapamamaktadır. Üçgenin çevresi için gerekli formülü verelim. Üç kenarı a,b,c olan üçgenin çevresi = a + b + c olur. Eğer üçgenin kenarları eşitse eşkenar üçgenin çevresi = a + a + a = 3a olur. Eşkenar üçgenle ilgili daha detaylı malumatı eşkenar üçgen konu anlatımından bulabilirsiniz. Üçgenin çevresi nasıl bulunur diye merak edenler için aslında bu kadar formül yeterlidir. Ancak özel üçgenlerde durum değişmektedir. Mesela iki kenar verilip üçgenin çevresi öyle istenmektedir. Bu durumda elde olan verileri kullanıp üçüncü kenarın uzunluğunu bulmak gerekir.
Dik üçgenin çevresi bulunurken eksik kenarlar Pisagor bağıntısı ile hesaplanır. Yine aynı şekilde eksik bir kenarı olan üçgenlerde çeşitli yükseklikler indirilerek eksik kenar tamamlanılabilir. Burada üçgenin çevresi derken kast edilen çoğu zaman bu tür problemlerdir. Yoksa üçgenin üç kenarını toplamak her öğrencinin yapabileceği bir şeydir. Şimdi eşkenar üçgenin çevresi ile ilgili bir örnek yapalım. Aşağıdaki eşkenar üçgende iki kenar uzunluğu bilinmeyen değerlerle ifade edilmiş ve çevre sorulmaktadır.
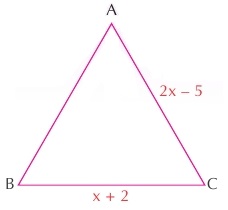
Bu soruda denklem eşitliğini kullanarak bir kenarı bulabiliriz. Eşkenar üçgenin kenarları eşit olduğuna göre x + 2 = 2x - 5 olur. Bu denklemi çözdüğümüzde x = 7 çıkar. İki kenardan birinde bu değeri yerine koyarsak da bir kenar uzunluğu 9 çıkar. Bu durumda eşkenar üçgenin çevresi 9.3 = 27 olur.
Üçgenin Çevresi ve Alanı
Üçgenin çevresi ile üçgenin alanı arasında doğrudan bir ilişki vardır. Üçgenin alanı konusunu bilmiyorsanız bu konuya çalışmalısınız. Biz burada sadece çevresi bilinen bir üçgenin alanını bulmayı göstereceğiz. Elbette ki üç kenar uzunluğu bilinen bir üçgende başka bir bilgi elimizde olmasa bile üçgenin alanını bulabiliriz. Çünkü kenarların uzunlukları bize üçgenin büyüklüğü ve kenarların birbirine bağlanma şekli açısından bilgiler vermektedir. Örneğin iki kenar ve bir açıyla kosinüs teoremiyle değer elde edebilir, sonra da sinüslü alan formülüyle alan hesaplayabiliriz. Ancak bunların hiçbirini yapmaya gerek yok. Çünkü bunlar hesaplanarak gerekli bir formül çıkarılmıştır. Bu formülü kullandığımız taktirde üçgenin çevresi yardımıyla alanını bulabiliriz.
Üçgenin çevresi = a + b + c = 2u olsun.
Üçgenin alanı √[u.(u-a).(u-b).(u-c)] olacaktır.
Üçgenin çevresi nasıl bulunur zaten yukarıda anlattık. Çevreden alana da bu şekilde geçilebilir. Tabi ki hiçbir açının bilinmediği sorularda bu yöntemi kullanmalısınız. Aksi taktirde mesela çevre tek sayı çıktığında u buçuklu bir değer çıkacak ve işlem yapmanız hayli zorlaşacaktır. Bu durumda aradaki bir açıyı bilirseniz sinüs alan formülü işinizi görecektir.
Kosinüs Teoremi İle Çevre Bulma
Kosinüs teorimi iki kenarı bilinen bir üçgende aradaki açı özel bir açıysa üçüncü kenarı bulmamızı sağlar. Bu durumda bütün kenarlar bilindiği için üçgenin çevresi kolaylıkla hesaplanabilir. Öğrencilerin birçoğu soruda üçgenin çevresi sorulduğunda bile üçüncü kenarı bulup cevaplardan o seçeneği işaretliyorlar. Dikkatsizlik maalesef geometri sorularında epey kaybettirmektedir.
Kenarları a, b ve c birim uzunlukta olan bir üçgende a ve b kenarıyla birlikte bu kenarların arasındaki açı da bilinmekteyse kosinüs teoremiyle c kenar uzunluğunu buluruz. Burada c2 = a2 + b2 - 2.a.b.cosα eşitliği vardır. Bunu bir örnek üzerinde test edelim.
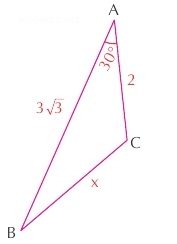
Yukarıdaki üçgende bize x uzunluğu sorulmaktadır. Bilinen iki kenar arasındaki açı ise 30 derece olarak verilmiştir.
Cos30 = Sin60 = √3/2 olduğunu bilmemiz gerekir.
x2 = 27 + 4 - 2.(3√3.2).(√3/2) olur. Buradan da x2 = 31 - 18 ⇒ x2 = 13 ⇒ x = √13 olacaktır.
Bu tarz sorularda kenarlar birbirinden farklı köklü ifadeler olduğu için genellikle çevre sorulmaz. Çevre sorularında çoğunlukla tam sayılı ifadeler kullanılır.
Etiketler:
Son Eklenenler
- Tarımla İlgili Meslekler
- Matematiği İyi Olmayanlar Hangi Mesleği Seçmeli?
- Antropoloji Nedir?
- Dünyanın Kaç Türlü Hareketi Vardır?
- Toplumsal Düzeni Sağlayan Kurallar Nelerdir?
- Cumhuriyet Yönetiminin Değerleri Nelerdir?
- İklim ve Hava Olayları Arasındaki Fark
- 1 Asal Sayı Mıdır?
- Homeostasi nedir?
- 2 ile Bölünebilme Kuralı
