Kökler Toplamı ve Çarpımı Bilinen İkinci Derece Denklemin Kuruluşu
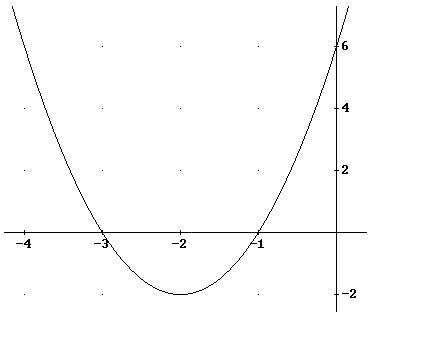
İkinci dereceden denklemler ortaöğretim düzeyinde en çok karşılaştığımız denklem tipidir. Kökler toplamı ve çarpımı bilinen ikinci derece denklemin kuruluşunu bugün öğreneceğiz. Bazen denklemin kökleri bilinmez fakat köklerin toplam ve çarpımı bilinir. Bu durumda bazı yöntemler kullanarak denklemi yazmaya çalışacağız. Verilmiş bir ikinci dereceden denklemin kökler toplamı ve çarpımını bulmak için bu ...
Okumaya devam etLogaritma Nedir?
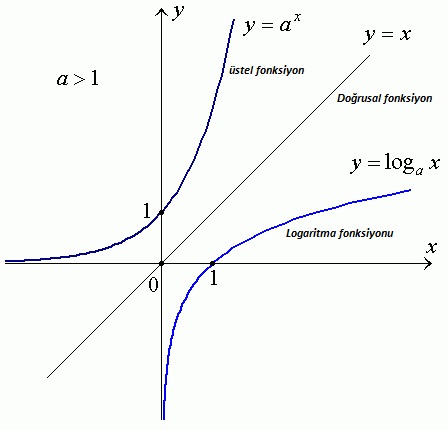
Matematik müfredatında gördüğümüz konulardan biri logaritmadır. Bu yazıda logaritma nedir onu inceleyeceğiz. Logaritmayla ilgili temel kuralları öğrenmek istiyorsanız logaritma konu anlatımı kısmından yararlanabilirsiniz. Logaritmayı anlamak için üstel fonksiyonu anlamak gerekir. Çünkü üstel fonksiyonla logaritma birbirine göre ters durumludur. Üstel fonksiyon bir reel sayının üssünün değişken olduğu fonksiyon türüdür. Örneğin f(x) = ...
Okumaya devam etSimetrik İki Kök
Denklem kökleriyle ilgili olarak “simetrik iki kök” kavramı karşımıza çok çıkmaktadır. Simetrik iki kökün ne olduğunu bilirsek soruları daha doğru yorumlarız. Soruda bize simetrik iki kökle verilmek istenen bir bilgi vardır. Öncelikle denklemde kök ne demektir ona değinelim. Yazıyı sonuna kadar okursanız çok önemli bir şeyi öğrenmiş olacaksınız. Denklemin Kökü Bir denklemin ...
Okumaya devam etKatsayılar Toplamı
Matematikte katsayılar toplamı sürekli karşımıza problem olarak çıkar. Bu konuyla ilgili matematikte çeşitli ezberler yapılır. Hepsinden önemlisi katsayılar toplamının ne olduğunu bilmektir. Matematikte katsayı, bilinmeyenin miktarını gösteren sayıdır. Örneğin 6x3 ifadesinin katsayısı 6’dır. 4x2 + 2x2 ifadesinin ise katsayılar toplamı 4 + 2 = 6’dır. Burada yapılan bir hata sabitin katsayısını ...
Okumaya devam etKöklü Sayılarda Sıralama
Köklü sayılarda sıralama matematikte köklü ifadeler konusu altında karşımıza çıkar. Bilenler için çok basit olan bu konu bilinmediği taktirde kafa karışıklığına neden olabilir. Karekök ifadelerinde sıralama yapmanın basit yöntemleri vardır. Bu yöntemlere kısaca değinelim. Kök İçine Atma Yöntemi İki sayıyı kıyaslamak için onların aynı durumda olmasını sağlamalıyız. Bu nedenle sıralayacağımız değerleri ya ...
Okumaya devam etEbob ve Ekok�un Genel Özellikleri
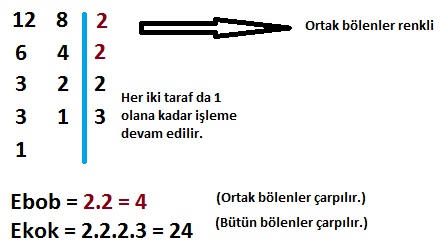
Matematikteki en önemli temel seviye konularından biri ebob ekok konusudur. Ebob ve ekokun genel özelliklerine girmeden önce ebob ve ekok nedir kısaca hatırlayalım. Ebob en büyük ortak bölen demektir. Eskiden matematik kitaplarında obeb yani ortak bölenlerin en büyüğü şeklinde yer alırdı. Ekok ise en küçük ortak kat demektir. Eskiden okek ...
Okumaya devam etHermann Minkowski ve Çalışmaları
Hermann Minkowski 22 Haziran 1864 ve 12 Ocak 1909 tarihleri arasında yaşamış bir Alman matematikçidir. Yahudi kökenli olan Minkowski, Almanya’nın önemli üniversitelerinde matematik ile uğraşmıştır. Hermann Minkowski 44 yaşında hayata veda etmesine rağmen çalışmaları ile matematiğe önemli katkılar yapmıştır. Minkowski sayı geometrisini yarattı ve geliştirdi. Geliştirdiği bu geometriyi sayı teorisi, ...
Okumaya devam et