Basit Harmonik Hareket

Bir cismi, yayın ucuna astığımızda cismin ağırlığından dolayı yay uzar. Fakat yay da asılı olduğu cisme yukarı doğ­ru bir kuvvet uygular. Bu yüzden cisim asıldıktan sonra, yayın ucu bir müddet aşağı ve yukarı hareket eder ve bir sü­re sonra durur. Bu durumda cismin ağırlığı ile yayda oluşan kuvvet dengede olur. Cismi yaydan ayırdığımızda yayın ucu yukarı doğru hareket eder. Eğer yayın ucundan ayırdığımız cisim daha ağır olursa yay yukarı doğru daha hızlı ha­reket eder. Bu durum yayın, kendisini geren cisme, eşit büyüklükte ve zıt yönde bir kuvvet uyguladığını gösterir.

Bir yaya kuvvet uygulayarak sıkıştırıp veya açtığımızda üzerinde potansiyel enerji depolanır. Bu enerji esneklik po­tansiyel enerjisi olarak da adlandırılır.

• Esneklik potansiyel enerjisi sıkıştırma veya gerilme miktarına ve maddenin esneklik özelliğine bağlıdır.
• Her yayın esneklik kat sayısı farklıdır. Bu kat sayı; yayın esnekliği, sertliği, yapıldığı maddenin cinsine ve yayın helezon sayısına bağ­lıdır.
• Esnekliğini kaybeden bir yay eski haline dönemez.

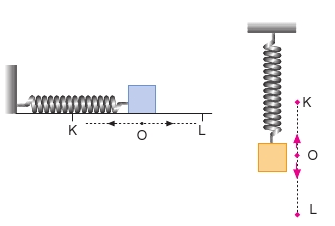
Şekildeki yayların uçlarına bağlanmış cisimler sürtünmesiz sistemde O denge konumundan biraz çekilip bırakıldık­larında iki eşit nokta arasında periyodik olarak gidip gelirler. Denge konumuna geri çağırıcı kuvvetlerin etkisi ile, sabit iki nokta arasında periyodik olarak gidip gelen cisimlerin hareketine basit harmonlk hareket denir.

Hormonik Harekette Temel Kavramlar

Genlik (r)

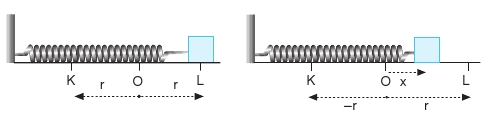
Basit harmonik hareketlinin denge noktasına olan maksimum uzaklığına denir. Şekildeki hare­ketlinin O denge noktasından olan maksimum uzaklıkları, |OK| = |OL| = r basit harmonik hareket­linin genliğidir.

Uzanım (x, y)

Basit harmonik hareketlinin herhangi bir anda denge noktasına olan uzaklığına uzanım denir. Maksimum uzanım genliktir. Minimum uzanım sıfırdır.

Periyot (T)

Basit harmonik hareket yapan bir hareketlinin bir noktadan aynı yönde ve art arda iki geçişi ara­sında geçen süreye periyot denir. Şekildeki hare­ketli her aralığı T/4 sürede alır.

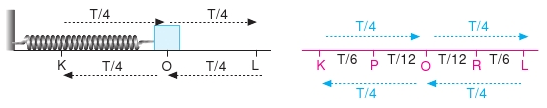
|KO| = |OL| uzunlukları iki eşit parçaya ayırdığımızda hareketlinin denge noktasına yakın olan kısmını T/12, uzak olan kısmını T/6 sürede geçtiği gözlenir.

Frekans (f)

Basit harmonik hareket yapan bir cismin bir saniyedeki titreşim sayısına frekans denir. Tıpkı dairesel hareket konusunda olduğu gibi, frekans ile periyot arasında f.T=1 ilişkisi vardır.

Dairesel hareket yapan bir cismin r yarıçaplı çember üzerinde­ki hareketi gösterilmiştir. Cisim L noktasından R noktasına geldi­ğinde yataydaki iz düşümü x, düşeydeki iz düşümü ise y dir. Ci­sim O noktasına geldiğinde düşeydeki iz düşümü y = r dir. Yatay­daki iz düşümü sıfır yani O^' noktasına gelmiş olur. Cisim tekrar T sürede L ye geldiğinde yatay iz düşümü K ile L arasında gidip gelme hareketi yapar. Cisim r yarıçaplı çember üzerinde dolanır­ken x ve y eksenleri üzerindeki dik izdüşümleri +r ve -r yarıçapla­rı arasında değişir. Bu harekete basit harmonik hareket denir.

Uzanım denklemleri yazılabilir. Maksimum uzanım genlik, minimum uzanım sıfırdır. Uzanım ifadesinin zamana bağlı grafiği şekildeki gibidir.

Türevin ve integralin Fiziksel Anlamı

Fiziksel olarak bir fonksiyonun türevini almak demek eğimini bulmak demektir, integralini almak demek de fonksiyonun altında kalan alanı bulmak demektir.

Konum-zaman grafiğinin eğimi (konumun zamana göre türevi) hızı, Hız-zaman grafiğinin eğimi (hızın zamana göre türevi) ivmeyi verir. İvme-zaman grafiğinin alanı (ivmenin zamana göre integrali) hızı, Hız-zaman grafiğinin alanı (hızın zamana göre integrali) konumu verir.

Hız Denklemi

Şekildeki cisim R noktasında iken hızın yatay ve düşey bile­şenleri alınırsa, V_x = -Vsinθ ve V_y = Vcosθ olur.

Cisim L noktasından R noktasına t sürede geldiğinde r konum vektörü θ açısını tarar. Bu açının bir saniyedeki radyan cinsinden değerine açısal hız (ω) demiştik.

Bu durumda hız denklemi iki yolla elde edilebilir.

ω = θ/t ⇒ θ = ω.t ve V = r.ω değerlerini yerine yazarsak. 

V_x = -rωsinωt  ve V_y = rωcosωt olur.

İkinci yol olarak da türevden gidebiliriz. Harekette yolun türevinin hızı verdiğini biliyoruz artık. 

x = r.cosωt ⇒ dx/dt = V_x = -rωsinωt ve y = r.sinωt ⇒ dy/dt = V_y = rωcosωt olur.

Gördüğünüz gibi iki yolla da hız denklemi elde etmek mümkündür.

Hareketli denge noktasından uzaklaştığında hareketlinin hızı azalır. Denge noktasına yaklaştığında hızı artar ve denge nokta­sında maksimum olur.

Hareketlinin hız-zaman grafiği şekildeki gibidir.

Hareketlinin denge konumundan x kadar uzaklıktaki hızının büyüklüğü,

V_x = ω.√(r² - x²) olarak bulunur. Hızın y bileşeni de,

Vy = ω.√(r² - y²) olarak elde edilir. Bu durumda V'nin büyüklüğü de V² = V_x² + V_y² olur.

İvme Denklemi

Hızın türevi ivmeyi verdiğine göre;

İvmenin yönü her zaman kuvvet ile aynı yöndedir. Şekilde bir basit harmonik hareketlinin herhangi bir andaki konum (x), kuvvet (F_x) ve ivme (a_x) vektörleri ile ivmenin zamana bağlı grafiği veril­miştir.

Kuvvet Denklemi

Basit harmonik harekette kuvvetin yönü her zaman denge nok­tasına doğru olduğundan bu kuvvete geri çağırıcı kuvvet denir. Di­namiğin temel prensibi buraya da uygulanır. Dinamikte kuvvet ivme ile kütlenin çarpımıdır.

Basit Harmonik Hareket Çeşitleri

Yay Sarkacı

Şekildeki sürtünmesiz ortamdaki yayların uçlarına m kütleli cisimler bağlanıp, denge konumlarından r kadar çekildiğinde K ve L noktaları arasında basit harmo­nik hareket yapar. Yayların cisimlere uyguladıkları kuvvete geri çağırıcı kuvvet denir. Bu kuvvet, F = -kx büyüklüğünde olup, (-) ifadesi kuvvet ile uzanım vektör­lerinin zıt yönlü olmasındandır. Yaya etki eden kuvvet aynı zamanda;

Yaylı sarkaçta periyodun kütle ve k yay sabitine bağlı grafikleri aşağıdaki gibi olur. Sürtünmesiz ortamda yaylı sar­kaçta periyotun büyüklüğü, cismin kütlesi ve k yay sabitine bağlıdır. Periyot; çekim ivmesi, uzanım genlik ve cismin bu­lunduğu yüzey veya düzleme bağlı değildir.

Yay Sarkacının Özellikleri:

• Kütle denge konumuna yaklaşırken ivme ve kuvvet azalır, hız artar. Denge konumundan uzaklaşırken kuvvet ve ivme artar, hız azalır.
• K ve L noktalarında hız sıfır, ivme maksimum, O noktasında hız maksimum, kuvvet ve ivme sıfırdır.
• Cisme etki eden kuvvet ve cismin ivmesi daima denge konumuna yöneliktir.
• Sarkacın genliği değişirse periyodu değişmez. Maksimum hız, ivme, kuvvet ve yaya aktarılan potansiyel ener­ji değişir.
• K ve L noktalarında enerji potansiyel enerji, O noktasında kinetik enerji ye eşittir.
• Kütle-yay sisteminin periyodu kütleye ve ucuna bağlandığı yayın esneklik sabitine bağlıdır.
• Yayın boyuna ve çekim ivmesine bağlı değildir.
• Kütle-yay sisteminin çekim ivmesinin farklı olduğu bir ortama götürülürse periyodu değişmez.

Basit Sarkaç

Ağırlığı ihmal edilen bir ipin ucuna m kütleli bir cisim bağlanıp O denge konumundan θ açısı kadar çekilip bırakıldığında cisim, K ve L noktaları ara­sında basit harmonik hareket yapar. Elde edilen sisteme basit sarkaç de­nir. Herhangi bir anda, bulunan cisme şekilde görüldüğü gibi G ağırlığını bi­leşenlere ayırdığımızda, G_x yörüngeye teğet, G_y dik olmak üzere iki bileşe­ni vardır.

G_x cismi yörüngede hareket ettiren geri çağırıcı kuvvet, G_y ise ipin geril­mesine sebep olan kuvvettir.