Kondansatörler (Sığaçlar)

Yüklü bazı iletkenleri birbirine yaklaştıracak olursak, bunların her birinin potansiyeli, sadece kendi taşıdığı yükle değil, etkileştiği öteki iletkenlerin yüklerinin cin­sine, miktarına, şekillerine, boyutlarına ve yerlerine bağlıdır. İki iletkenden ve aralarındaki yalıtkan bir ortamdan mey­dana gelen sisteme kondansatör ya da sığaç denir.

Kondansatörler elektrik yükü de­polamaya yarayan düzeneklerdir. Kondansatörlerdeki iletken levha­lara armatör denir. Armatörleri düzlem levha şeklinde olan kon­dansatörlere düzlem kondansa­törler denir.

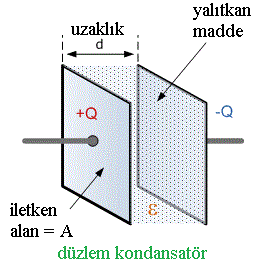
Düzlem kondansatörler üretece bağlanarak da yüklenebilir. (+) kutba bağlanan levha (+), (-) yüklü kutba bağlanan da (-) yükle yüklenir. Kondansatörlerin uçları arasında­ki potansiyel farkı üretece bağlı olduğu sürece ürete­cin uçları arasındaki potansiyel farkına eşittir.

Bir kondansatörün yükü denildiğinde işaretine bakıl­maksızın, levhaların birindeki yük miktarı anlaşılır.

Sığa

Bir kondansatörün yükünün, yükün kondansatöre ka­zandırdığı potansiyele oranı sabittir. Bu sabit değere kondansatörün sığası denir. Buna göre sığa;

C = q/V bağıntısıyla bulunur. Burada

q: İletkenin yükü (coulomb) 

C: İletkenin sığası (farad) 

V: İletkenin potansiyeli (volt) dir.

Sığa, volt başına düşen coulomb olarak da tanımlana­bilir. SI birim sisteminde sığa birimi farad’dır. Farad bü­yük bir sığa birimi olduğundan, pra­tikte genellikle mikrofarad ve pikofarad birimleri kullanılır.

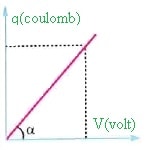
Bir iletkenin sığası sabit ise, yü­kü ile potansiyeli doğru orantılı­dır. Yükün potansiyeline göre de­ğişim grafiği, şekildeki gibi olur. Doğrunun eğimi ise iletkenin sı­ğasını verir.

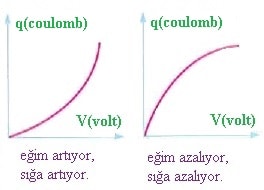
Eğer eğim artıyor­sa sığa artıyor, eğim azalıyorsa sı­ğa da azalıyor de­mektir. Yalnız ilet­kenin sığası hiç bir zaman sıfır olmaz. Yani burada eği­min sıfır olması durumunda sığa da sıfır olmaz.

Kondansatörün Yapısı

Yükü q, levhaların uçları arasındaki potansiyel farkı V ise kondansatörün sığası, C = q/V dir.

Bir düzlem kondansatörün levhalarından birinin yüzey alanı A, lev­halar arası uzaklık d ve levhalar arasındaki yalıtkan ortamın dielektrik sabiti ε ise, kondansatörün sığası,

C = ε.A/d bağıntısıyla bulur.

Bu bağıntıya göre A, d ve ε niceliklerinden biri ya da bir kaçı değiştirilirse yani kondansatörün yapısında bir değişiklik olursa sığa değişir. Yükün ya da potansiyel farkının değişmesi ile sığa değişmez.

Boş uzayın elektriksel geçirgenliği,

ε₀ = 8,85.10^-12.C²/N.m²

Kondansatör adını sığası bilinen belli bir düzenek için kullandık. Öte yandan herhangi bir iletkenin de aynı yoldan tanımlanan bir sığası vardır. Fakat böyle bir ilet­kene kondansatör denilemez.

Kondansatör Çeşitleri ve Kullanım Alanları

Kondansatörler genel olarak elektrostatik de­neylerinde, al­ternatif akımda radyo, televiz­yon ve bilgisa­yar gibi elektro­nik devrelerde kullanılır. İçinde­ki yalıtkan cinsine göre çeşitleri vardır.

Yüklü Bir Kondansatörün Enerjisi

Bir kondansatörü yüklerken, alçak potansiyeldeki lev­halardan yüksek potansiyeldeki levhaya yük taşın­maktadır. Bunun için ise elektriksel kuvvetlere karşı bir iş yapmak gerekmektedir.

Başlangıçta yüksüz olan levhalar arasındaki potansi­yel farkı sıfırdır. Kondansatör yüklenip q kadar yük taşıdıktan sonra, levhalar arasındaki potansiyel farkı V değerine ulaşır.

Burada, q = C.V bağıntısı vardır. Daha önceki bağıntıyı düzenlersek bu bağıntıyı rahatlıkla elde edebiliriz. Bu bağıntıdan anlaşıldığı gibi q arttıkça V artar. Yani iki değer doğru orantılıdır. Doğru orantılı q - V grafiğinin altında kalan alan yapılan işi, dolayısıyla da depolanan enerjiyi verir.;

E = q.V/2 grafikte alanı veren bağıntıdır. Burada q yerine C.V yazarsak E = 1/2.C.V² bağıntısını elde ederiz.

Burada,

E: Kondansatörde depolanan enerji (joule)

C: Kondansatörün sığası (farad)

V: Kondansatörün uçları arasındaki potansiyel farkı (volt)

Kondansatörler DC gerilimde (doğru gerilim)dolup boşalma yöntemiyle çalışır. Tam dolduğunda açık devre gibi davranır. Yani akım sıfır olur.

AC gerilim (alternatif gerilim) uygulandığında ise di­renç gibi davranır. Bu direncin değeri gerilimin fre­kansına ve kondansatörün sığasına bağlıdır. Fre­kans arttıkça direnç azalır, frekans azaldıkça direnç artar.

Kondansatörlerin Bağlanması

Seri bağlama ve özellikleri

İki ya da daha fazla kondansatörün aynı yük kolu üzerinde olacak biçimde bağlanmasına seri bağlama denir.

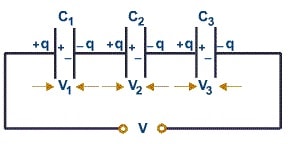
Şekildeki devrede sistemin iki ucu arasına V potansiyel farkı uy­gulanırsa, C₁ sığalı kondansatör +q yükü ile yüklenir. Bu +q yükü C₂ sığalı kondansatörden -q kadar yük çeker ve C₂ sığalı kondansatör +q kadar yükle yüklenir. Bu da C₃ sığalı kondansatöründen -q kadar yük çeke­rek onun da + q yükü ile yüklenmesine neden olur.

Böylece C, ve C₃ sığalı kondansatörlerin en dıştaki levhalar üreteçten yüklenmiş, diğer levhalar ise etki ile yüklenmiş olur.

Buna göre seri bağlı kondansatörlerin sığaları ne olur­sa olsun her birinin yük miktarı eşittir. Toplam yük ise kondansatörlerden birinin yüküne eşittir.

Aynı potansiyel farkı altında, toplam yük kadar yük de­polayan sığaya eşdeğer sığa denir.

Özellikler

1. Her bir kondansatörün yükleri eşit ve toplam yük birinin yüküne eşittir. q_T = q₁ = q₂ =q₃
2. Üç kondansatörün uçları ara­sındaki V potansiyel farkı, her bir kondansatörün uçları arasındaki potansiyel farkları­nın toplamına eşittir. V = V₁ + V₂ + V₃
3. Devrenin eşdeğer sığasının tersi, sığaların tersleri­nin toplamına eşittir. Eşdeğer sığa, 1/C_eş = 1/C₁ + 1/C₂ + 1/C₃ bağıntısıyla bulunur.
4. Eğer sığaları C₁ ve C₂ olan iki kondansatör se­ri bağlanmış ise eşdeğer sığa, C_eş = C₁.C₂/(C₁ + C₂) bağıntısıyla bulunur.

Bu şekilde ikişerli eşdeğer sığa bulmak işlem ko­laylığı sağlar.

Seri bağlı ve sığaları eşit n tane kondansatör seri olarak bağlanırsa devrenin eşdeğer sığası, bir kondansatörün sığasının, kondansatör sa­yısına bölümünden bulunur. C_eş = C/n

Seri bağlı kondansatörlerin eşdeğer sığasının değeri, en küçük sığanın değerinden daha kü­çüktür. Örneğin 20 μF, 10 μF ve 1μF sığalı ve seri bağlı üç kondansatörün sığası en küçük sığa olan 1μF'dan daha küçüktür.

Paralel bağlama ve özellikleri

İki ya da daha fazla kondansatörün birer uçları bir noktaya bağlanarak elde edilen bağlama şekline paralel bağlama denir.

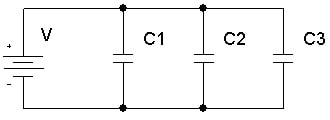
Paralel bağlı kondansatörlere V gerilimi uygulanırsa bütün kondansatörlerin gerilimi de yine V olur. Üretecin (+) kutbuna bağlı tarafı pozitif yüklü, (-) kutbuna bağlı tarafı ise negatif yükle yüklenir. 

Özellikler

1. Her bir kondansatörün uçları aynı noktalara bağlandığı için uçları arasındaki gerilimler aynı olur. V = V₁ = V₂ = V₃
2. Kondansatörlerin uçları arasındaki gerilimler eşitken sığalar farklı olduğu için yükler de farklı olur. Bu yüklerin toplamı toplam yüke eşittir. q_T = q₁ + q₂ + q₃
3. Eşdeğer sığaların toplamı toplam sığayı verir. Buna göre eşdeğer sığa, C_eş = C₁ + C₂ + C₃ bağıntısı ile bulunur.

Ortak Potansiyel

Yükleri, gerilimleri ve sığaları farklı iki kondansatör iletken bir tel ile birbirine bağlanırsa paralel bir devre kurulur. İlk durumda potansiyelleri eşit olmayan bu iki kondansatörden potansiyeli yüksek olan düşük olana doğru yük geçişi olur. Son durumda potansiyeller eşitlenir. Her iki kondansatörün sahip olduğu bu eşit potansiyele ortak potansiyel denir. 

Ortak potansiyel toplam yükün toplam sığaya oranıdır. Kondansatörler paralel ise ΣC = C₁ + C₂ olur.

Eğer yüklü bir kondansatör boş bir kondansatöre bağ­lanırsa, aynı bağıntı geçerlidir. Fakat boş olan kondan­satör bağlanmadan önce yüklü olmadığından q₂ yeri­ne sıfır yazılır. Burada q₂ = 0 olsa da C₂’nin sıfır olma­dığına dikkat edilmelidir.

Ayrı ayrı yüklenen kondansatörlerin levhaları ters bağ­lanırsa, yani birinin (+) levhası diğerinin (-) levhasına bağlanırsa, önce levhaların yüklerinden nötrleşme olur tekrar ilk kısımda anlatılan şekle dönüşür.

Kondansatörün sığasının nelere bağlı olduğunu söyledik. Bir kondansatör üretece bağlı İken levhalar arası uzaklık artırılırsa ya da azaltılırsa sığa başta verdiğimiz bağıntıya göre değişir. Ancak üretecin ve kondansatörün uçları arasındaki potansiyel fark sabittir. 

q = C.V bağıntısına göre, V sabit ise C'nin değişmesi oranında q da değişir.

Eğer kondansatör üretece bağlı değilse, bu durumda levhalardaki yük sabittir. q = C.V bağıntısına göre q sabitse, C ile V ters orantılı şekilde değişir. Kısacası bu bağıntıyı tüm durumlar için kullanabilirsiniz. Tüm sistem için ve tek tek kondansatörler için de yine bu bağıntı geçerli olur.