Yamuk
Alt ve üst kenarları birbirine paralel olan dörtgenlere yamuk denir. Yamuk özel dörtgenlerden biridir. Şekline baktığınız zaman sıradan bir dörtgen gibi görünür. Yamuk ile sıradan bir dörtgenin farkı yamuÄŸun iki kenarının paralel olmasıdır.
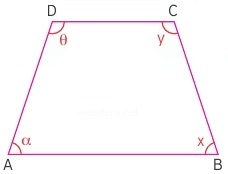
Şekilde ABCD yamuÄŸu verilmiÅŸtir. [AB] // [DC] kenarlarının paralellik durumu dörtgeni yamuk yapmaktadır. ParalelliÄŸin sonucu olarak x + y = 180° eÅŸitliÄŸi vardır.
Yamuk Özellikleri
Yamuk özellikleri bilinirse yamuk özelliÄŸi taşıyan geometrik ÅŸekillere daha doÄŸru bir yaklaşım sergilenebilir. YamuÄŸun en önemli özelliÄŸi iki kenarın paralel olmasıdır.
Soru: Her paralelkenar bir yamuk mudur?
Cevap: Paralelkenarın kenarları paralel olduÄŸuna göre elbette yamuktur. DiÄŸer iki kenarın da paralel olması bu durumu deÄŸiÅŸtirmez. Paralelkenar, eÅŸkenar dörtgen, dikdörtgen, kare gibi çokgenlerin hepsi yamuk olma özelliÄŸini de taşırlar aynı zamanda.
Yamukta Açılar
Yamukla ilgili en önemli durum paralelliktir. ParalelliÄŸin sonucu olarak da paralel açılar bütünlerdir. Bu konuda açı ile ilgili karşımıza çıkan durumların geneli bunla ilgidir. Şimdi yamukta açılar ile ilgili bir örnek yapalım ve paralelliÄŸi nasıl kullanacağımızı görelim.
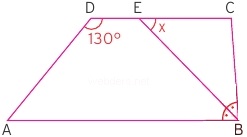
Soru: Yukarıdaki ÅŸekilde yamuk içerisinde bir üçgen verilmiÅŸtir. Aynı zamanda C açısı A açısının 2 katıdır. Buna göre x açısın kaç derece olduÄŸunu bulunuz.
Çözüm: Yamukta paralellikten dolayı iç ters açı durumları oluÅŸmuÅŸtur. Bu nedenle x açısını aynı ÅŸekilde aÅŸağı yazabiliriz.
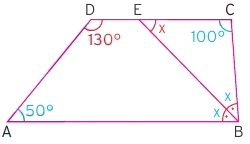
Yine paralellikten dolayı D ve A açıları bütünler açılar olacaktır. D açısı 130 derece olduÄŸuna göre A açısı 50 derece olacaktır. C açısı ise A açısının 2 katı olduÄŸundan 100 derece olacaktır.
Sonuçta ortaya çıkan üçgende 100 + 2x = 180 eÅŸitliÄŸi kurulur. Buradan da x = 40° bulunur.
Yamukta Orta Taban
Yamukta paralel olan iki kenar çoÄŸunlukla eÅŸit uzunluk olmaz. Ä°ki kenarın da aritmetik ortalamasına sahip orta taban dediÄŸimiz hayali bir çizgiye ihtiyaç duyarız. Orta taban uzunluÄŸu aritmetik uzunluk olduÄŸu için konumu da iki kenarın ortasında olur.
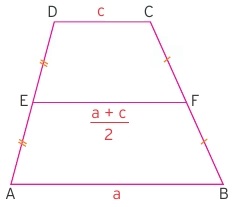
Yukarıdaki yamukta E ve F noktaları bulundukları kenarların orta noktalarıdır. Bu durumda [EF] doÄŸru parçası orta taban olur. |EF| uzunluÄŸu ise iki paralel kenarın aritmetik ortalamasına eÅŸittir. Orta taban da haliyle bu kenarlara paralel olacaktır.
|AB| = a, |DC| = c ⇒ |EF| = (a + c) / 2 olur.
Yamukta orta tabanı anlamak için çok basit bir örnek yapalım.
Örnek: AÅŸağıdaki yamukta kenarların orta noktaları birleÅŸtirilerek bir doÄŸru parçası elde edilmiÅŸtir. Bu doÄŸru parçasının uzunluÄŸu nedir?
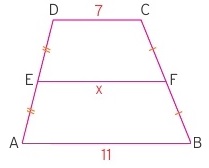
Çözüm: Orta noktalar birleÅŸtirildiÄŸine göre ortaya çıkan doÄŸru parçası orta taban olacaktır. Bu durumda uzunluk 11 ve 7'nin orta noktası olan 9 olacaktır.
Yamukta KöÅŸegen ve Orta Taban Ä°liÅŸkisi
Yamuk için en önemli özelliÄŸin paralellik olduÄŸunu söyledik. Orta taban ve köÅŸegen çizilirse paralellikten dolayı ortaya çıkan üçgenlerde benzerlik teori uygulayabiliriz. Orta taban iki kenarı da iki eÅŸit parçaya ayırdığı için benzerlik oranı da 1'e 2 olacaktır.
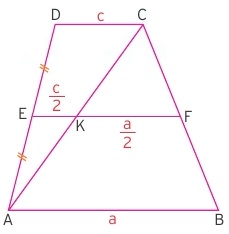
Yukarıdaki yamukta orta taban ve köÅŸegenlerden biri çizilmiÅŸtir. Burada orta tabanda bölüne parçaların yamuk tabanlarının oranının 1/2 olduÄŸu görülmektedir.
Yamukta Alan
Yamuk ile ilgili diÄŸer bir husus yamukta alan hesabıdır. Yamukta alan ile orta taban arasında sıkı bir iliÅŸki vardır. Elbette bütün dörtgenlerde olduÄŸu gibi burada da bir yüksekliÄŸe ihtiyaç duyarız. Yükseklik olduktan sonra yamuÄŸu iki üçgene ayırıp alanı hesaplanabilir. Ancak iki kenarın ortalaması deÄŸerinde olan orta tabanı yükseklikle çarptığımızda alanı doÄŸrudan elde ederiz.
YamuÄŸun alanı = Orta taban x yükseklik
YamuÄŸun alanı ile ilgili edindiÄŸimiz temel bilgiyi basit bir örnekte uygulayalım.
Örnek: AÅŸağıdaki yamukta paralel kenar uzunlukları 4 ve 6 birim olarak verilmiÅŸtir. YüsekliÄŸi de 8 birim olarak verilen bu yamuÄŸun alanı kaç birim2 olur?
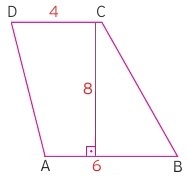
Çözüm: YamuÄŸun alanı için elimizde yükseklik olduÄŸuna göre orta tabana ihtiyacımız vardır. Orta taban uzunluÄŸu paralel iki kenarın aritmetik ortalamasıydı. Öyleyse orta taban = (4 + 6) / 2 = 5 olur.
Yükseklik = 8 birim olduÄŸundan, alan = 8.5 = 40 birim2 bulunur.
EÄŸer orta tabanı hesaplamasaydık o zaman iki üçgene ayırıp alanı hesabı yapmamız gerekirdir. Ä°ki üçgenin alanını da aynı yükseklik deÄŸeriyle hesaplayacaktık. Herhangi bir köÅŸeden çizdiÄŸimizde taban uzunlukları 4 ve 6 birim olan, yüksekliÄŸi ise 8 birim olan iki üçgen elde edecektik.
Bu durumda alan = 4.8/2 + 6.8/2 = 40 bulunacaktı. GördüÄŸünüz gibi alan hesabını verilen duruma göre orta taban ile ya da üçgenlere ayırarak yapabilmekteyiz.
Orta tabanla ilgili bilmemiz gereken bir özellikte yüksekliÄŸi de iki eÅŸ parçaya ayırmasıdır. Bunu bir kural olarak deÄŸil mantık olarak bilmemiz gerekir.
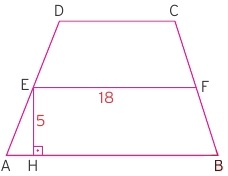
Yukarıdaki ÅŸekilde orta taban uzunluÄŸu 18 cm olarak verilen bir yamuÄŸun orta taban ile kenar arasındaki dikmenin uzunluÄŸu da 5 cm olarak verilmiÅŸtir. Bu durumda yamuÄŸun alanı kaç cm2 olur?
YamuÄŸun alanı sorulduÄŸuna göre orta taban ve yüksekliÄŸe ihtiyacımız vardır. Orta taban elimizde veri olarak bulunuyor. Yükseklik de orta tabandan çizilmiÅŸ bir ÅŸekilde verilmiÅŸtir. Öyleyse yamuÄŸun yüksekliÄŸi orta tabandan indirilen dikmenin iki katı olacaktır. Yani yamuk yüksekliÄŸi 10 cm olacaktır.
Bu durumda yamuÄŸun alanı = Yükseklik x orta taban = 10x18 = 180 cm2 bulunur.
Yamukta Alan Oranları
Yamukta köÅŸegenleri çizersek ortaya çıkan ÅŸekillerde benzerlik oranıyla uyuÅŸacak ÅŸekilde alan oranları elde edilir.
Yamukta köÅŸegenler sonucunda ortaya çıkan dört üçgenden ikisinin alanı eÅŸit olur. DiÄŸer iki üçgenin alanları ise benzerlik oranının karesiyle orantılıdır. Alan çarpım sonucu olarak ortaya çıkan iki boyutlu bir özellik olduÄŸundan deÄŸeri de benzerlik oranının karesiyle orantılı olmak durumundadır.
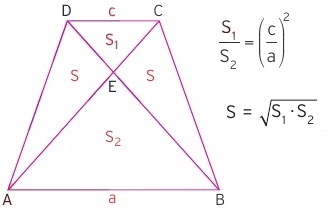
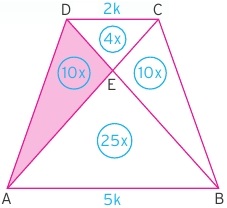
Yukarıdaki ÅŸekilde yamukta alan oranları ile ilgili temel bilgiler verilmiÅŸtir. AÅŸağıdaki ÅŸekilde ise alan oranları rakamlarla örneklendirilmiÅŸtir.
Ä°kizkenar Yamuk
Yamuklar içerisinde özel yamuk diyebileceÄŸimiz örnekler vardır. Bunlardan ilki ikizkenar yamuk ÅŸeklidir. Ä°kizkenar yamuk paralel olmayan kenarların eÅŸit uzunlukla olmasıyla ortaya çıkar. Ä°kizkenar yamukta eÅŸit kenar eÅŸit açı manasına da gelmektedir.
Ä°kizkenar yamukta eÅŸit kenarların tabanlarla yaptığı açılar eÅŸit olur. Bu nedenle köÅŸegenler ile ortaya çıkan üçgenlerde de çeÅŸitli eÅŸitlikler ortaya çıkar.
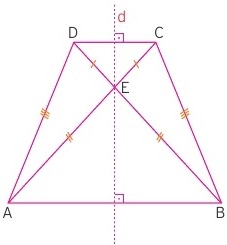
Yukarıda bir ikizkenar yamuk üzerinde eÅŸitlikler gösterilmiÅŸtir. EÅŸitlikten dolayı oluÅŸan simetri de dik çizilen d doÄŸrusu ile gösterilmiÅŸtir. Bu doÄŸru köÅŸegenlerin kesim noktasından geçer ve yamuÄŸun simetri eksenidir.
Dik Yamuk
Özel yamuklar içerisinde diÄŸer bir geometrik ÅŸekil dik yamuk dediÄŸimiz ÅŸekildir. Burada kenarların birisi paralel kenarlara diktir. Kısmen yamuÄŸa göre daha düzenli bir ÅŸekil elde edilmiÅŸtir.
Dik yamuk sorularında uzunluk ve açı hesabı yaparken verilen dikmenin karşısında paralel bir dikme çizmek çok önemlidir.
Dik yamukta dik kenar aynı zamanda yamuÄŸun yüksekliÄŸi manasına gelir. DoÄŸal olarak alan hesabı bu kenar ile yapılır.
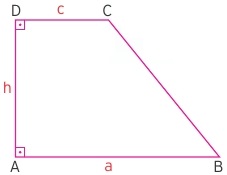
Yukarıdaki ÅŸekilde en klasik haliyle bir dik yamuk örneÄŸi verilmiÅŸtir. YamuÄŸun kısa kenar c uzun kenarı da a birimdir. YüksekliÄŸin h birim olduÄŸuna göre alan = h.(a + c)/2 formülü ile bulunacaktır.
