Üçgende Açı Kenar Bağıntıları
Üçgende açı kenar bağıntıları konusu ile üçgende açı ve kenar uzunlukları arasındaki ilişkiyi incelemekteyiz. Nispeten kısa olan açı kenar bağıntıları konusu neredeyse her sınavda çıkması itibariyle önemlidir.
Bir üçgende büyük açının karşısında büyük kenar, küçük açının karşısında küçük kenar bulunur. Bir üçgendeki en büyük kenar en geniş açının karşısında bulunandır. Buradan şu sonucu çıkarabiliriz. Eğer geniş açılı bir üçgenimiz varsa kesinlikle üçgen içerisindeki en büyük kenar geniş açının karşısında olan olacaktır.
Dik üçgende en büyük açı dik açı olan 90 derece olduğu için dik açı karşısındaki kenar (hipotenüs) doğal olarak en uzun kenar olmaktadır.
Üçgende açı kenar bağıntıları üçgen içerisinde geçerlidir. Kıyaslama iki üçgen arasında yapılırsa yanılma gerçekleşebilir. Çünkü büyük çizilmiş bir üçgende 30 derece karşısına gelen kenar daha küçük çizilmiş bir üçgende 120 derecenin karşısındaki kenardan daha uzun olabilir. Bu nedenle kıyaslama üçgen içerisinde yapılmalıdır.
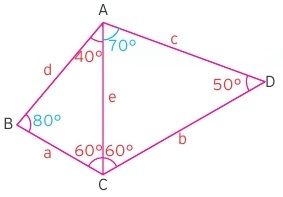
Yukarıdaki üçgende en uzun ve en kısa kenarı bulalım. Sol tarafa baktığımız zaman en uzun kenarın e kenarı olduğunu fark ederiz. Ancak sağ taraftaki üçgende e kenarından daha uzun b ve c kenarları bulunmaktadır. Sağ taraftaki üçgende en büyük kenar b kenarı olduğu için sistemin en büyük kenarı da b kenarı olacaktır. Dikkar edersek 70 derecenin karşısına gelen kenar 80 derecenin karşısına gelenden büyük olmaktadır. Çünkü farklı üçgenler için birebir açı kıyaslaması yapılamaz.
Sistemin en kısa kenarına gelecek olursak sağdaki üçgenin en kısa kenarı 50 derecenin karşısındaki e kenarıdır. Ancak soldaki üçgende bu 80 derecelik açıya denk gelen en uzun kenar olmaktadır. Bu nedenle soldaki üçgendeki en kısa kenar olan 40 derecenin karşısındaki a kenarı sistemin en kısa kenarı olmuş olur.
Üçgenin Çizilebilmesinin Temel Şartı
Bir üçgenin çizilebilmesi için bazı şartların yerine gelmesi gerekmektedir. Üçgende herhangi iki kenarın uzunluğunun toplamı diğer kenarın uzunluğundan fazla olmak zorundadır. Yine aynı şekilde iki kenar uzunluğunun farkı ise diğer kenardan daha az olmak durumundadır. Bu kuralı sağlamayan üçgenler üçgen olamazlar. Çünkü bu kural üçgen çizilebilmesinin temel şartı olarak karşımıza çıkar. Buna üçgen eşitsizliği denir.
Açı kenar bağıntıları konusunda üçgen eşitsizliği sorularının önemli bir payı vardır. Bu nedenle bu basit konuyu iyi anlamak gerekir. Şimdi üçgen eşitsizliği ile ilgi bir örnek yapıp öğrendiklerimizi uygulayalım.
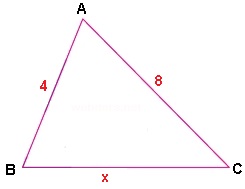
Yukarıdaki üçgende iki kenarı 4 ve 8 birim olarak verilen bir üçgende üçüncü kenar uzunluğu x ile gösterilmiştir. Buna göre x'in alabileceği tam sayı değerleri nelerdir?
Çözüm: Soruda üçgen eşitsizliği kuralının uygulanması istenmektedir. Bu kurala göre iki kenarın toplamı kesinlikle üçüncü kenardan büyük olmalıdır. Yine aynı şekilde iki kenarın farkı da üçüncü kenardan küçük olmalıdır.
Buna göre şu sonuç karşımıza çıkar: |8 - 4| < x < |8 + 4| ⇒ 4 < x < 12 ⇒ x = {5, 6, 7, 8, 9, 10, 11}
Gördüğünüz gibi x burada 5'ten 11'e kadar olan tam sayı değerlerini alabilmektedir. Peki x neden 4 olamaz? Bir kenar zaten 4 iken diğer kenar bu üçgende neden 4 olamamaktadır?
Bu sorunun cevabı aslında biraz mantığınızda yatmaktadır. B köşesinden iki tane 4 birim uzunluğunda doğru parçası çıksa ve bunların uçları şekildeki üçgen gibi birleştirilse, bu birleşen kenarın 8 birim olabilme ihtimali yoktur. Mutlaka 8'den küçük olmak zorunda kalacaktır.
Açı Kenar Bağıntılarında Pisagor
Pisagor bağıntısı geometrideki en önemli bağıntı olması nedeniyle her konuda karşımıza çıkabilmektedir. Burada da yine aynı şekilde Pisagor bağıntısı ile birlikte açı kenar bağıntılarını değerlendireceğiz.
Pisagor bağıntısında a2 = b2 + c2 olduğunu biliyoruz. Bu şartın sağlanması için a kenarı karşısındaki açısın 90 derece olması temel şarttır. Şimdi aşağıdaki üçgene bakalım.
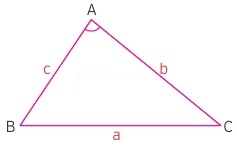
Burada A açısının 90 olma dışındaki iki ihtimalini de değerlendirmeliyiz.
Eğer A > 90 a2 > b2 + c2
Eğer A < 90 a2 < b2 + c2 olur.
Burada açı kenar bağıntılarının temel mantığı yine geçerli olmaktadır. Bunu bir örnekle pekiştirelim.
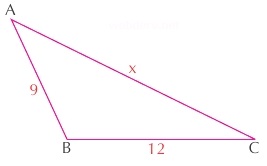
Yukarıdaki üçgende ABC açısının geniş açı (90 dereceden büyük) olduğu bilinmektedir. Buna göre x'in alabileceği tam sayı değerleri nelerdir?
Çözüm: Pisagor bağıntısında 9 - 12 - 15 üçgeni diye bir özel üçgen olduğunu biliyoruz. Öyleyse burada da B açısı 90 derece olsaydı x 15 olacaktı. Ancak bu açı 90 dereceden büyük olduğu için x de 15'den büyük olacaktır.
Üçgen eşitsizliği kuralını da dahil edersek 15 < x < |9 + 12| ⇒ x = {16, 17, 18, 19, 20} olur.
Neden Büyük Açı Büyük Kenar Demektir?
Büyük açının karşısında büyük kenar küçük açının karşısında küçük kenar olduğunu öğrendik. Zaten üçgende açı kenar bağıntılarının temeli bunun üzerine kurulmuştur. Bunun ispatini şu şekilde yapabiliriz. İki elinizi gergin hale getirin. Sonra da bilekleriniz karşılıklı birbirine değecek şekilde iki elinizi v harfi şeklinde birleştirin. Bu durumda iki elinizin arasında açısal bir bölge oluşmaktadır.
Orta parmaklarınızın uçları arasında bir bağlantı olduğunu hayal edin. Bu bağlantı bizim üçgenimizin son kenarı olsun. Elinizi birbirine yaklaştırıp uzaklaştırın. Böylece açıyı genişletip daraltmış olursunuz. Dikkat ederseniz açı daraldığında parmak uçlarınız birbirine yaklaşmakta, tersinde ise uzaklaşmaktadır. Açı kenar bağıntılarının temel mantığı işte burada toplanmaktadır.
