Eşkenar Üçgen

Üç kenarının uzunluğu da eşit olan üçgene eşkenar üçgen denir. Kenarların hepsinin eşit olması açıların hepsinin de eşit olmasını beraberinde getirir. Üçgenin iç açıları toplamı 180 derece olduğuna göre eşkenar üçgenin her bir açısı 60 derecedir sonucuna varabilir. Eşkenar üçgen öğrenciler tarafından çok sevilen bir üçgen tipidir. Çok fazla eşitlik olması işlemleri kolaylaştırır ve bizi kolay hedefimize götürür. Kısacası eşkenar üçgen en düzgün üçgendir diyebiliriz.

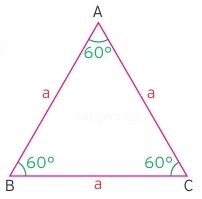
İkizkenar üçgen için geçerli her özellik eşkenar üçgende de aynen geçerli olacaktır. Çünkü eşkenar üçgende de iki eşit kenar bulunur. Ekstradan sadece diğer kenar da eşittir. Dolayısıyla üçgen içerisinde indirilen dikmenin hem yükseklik, hem açıortay hem de kenarortay olması burada da geçerlidir.

Eşkenar Üçgenin Yüksekliği

Üçgende yükseklik çizdiğimiz zaman üçgenin temel özelliklerini de elde etmiş oluruz. Bu nedenle eşkenar üçgenin yüksekliği önemlidir. Yükseklik bize kenarlar arasındaki oranları da verecektir.

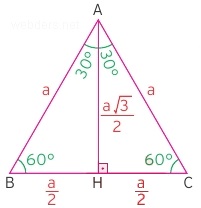
Eşkenar bir üçgenin her bir kenarına a birim dersek. Yükseklik de a'nın yarısın √3 katı olacaktır. Ortaya aynı zamanda 30 - 60 - 90 üçgeni de çıkacaktır. Tamamen simetrik ve özellikleri belirlenmiş bu üçgende yüksekliği hangi köşeden çizerseniz çizin sonuç değişmeyecektir.

Yukarıdaki şekli iyice zihninize oturttuğunuz taktirde eşkenar üçgen sorularında hiçbir problem yaşamazsınız. Aslında böyle bir görünüm bu konuyu özetlemektedir. 

Eşkenar üçgende işlem yapmaya başlamadan önce her açının 60 derece olduğunu belirtmek için açıları üçgen içerisine yazın. Bunu yaptığınızda bir şeyleri gözden kaçırmanız daha zor hale gelecektir.

Soru: Yüksekliği 2√3 cm olan eşkenar üçgenin çevresi kaç  cm dir?

Çözüm: Yükseklik bir kenar uzunluğunun yarısının √3 katı kadardır. Bu durumda bir kenar 4 cm olacaktır. Üçgenin çevresi de 4x3 = 12 cm olacaktır.

Eşkenar Üçgende Yardımcı Özellikler

Eşkenar üçgende yardımcı birçok özellik bulunmaktadır. Bu özelliklerin birçoğu birbiri ile doğrudan bağlantılı olduğu için hepsinin üzerinde durmayacağız. Zaten ikizkenar üçgende geçerli olan her şey eşkenar üçgen için de geçerlidir.

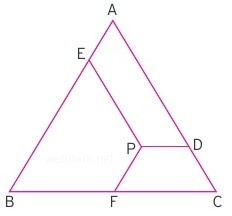
ABC eşkenar üçgenin içerisinde herhangi bir p noktası seçelim. Bu p noktasından kenarlara karşı kenara paralel olacak şekilde üç tane doğru parçası çizelim. Elde edilen üç doğru parçasının uzunluklarının toplamı üçgenin bir kenarının uzunluğuna eşittir.

Yani |PD| + |PE| + |PF| = |AB| = |AC| = |BC| olur.

Yukarıdaki eşkenar olduğu bilinen üçgende içerideki doğru parçalarının hepsi karşı kenarlara paraleldir. Buna göre bu üçgenin çevresi kaç birimdir?

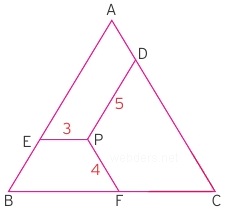
Çözüm: Paralel doğru parçalarının toplamı bir kenarın uzunluğuna eşittir. Buna göre bir kenar uzunluğu 3 + 4 +5 = 12 olur. Üçgenin çevresi ise 3.12 = 36 birim olur.

Özel Üçgen Soruları

Açılarından biri 30°, 45°, 60°, 120°, 135° ve 150° olan üçgenleri özel üçgenler olarak isimlendiriyo­ruz. Bu üçgenlerle ilgili olan soruları çözerken 30° - 60° - 90° ve 45° - 45° - 90° üçgenlerinin kenar özelliklerinden faydalanırız. Eğer açımız 30°, 45° veya 60° gibi dar bir özel açı ise, açının karşısına dikme inerek, 120°, 135° veya 150° gibi bir geniş açı ise, açının bütünlerini oluşturduktan sonra dış açının kollarından birine dikme ineriz. Daha sonra Pisagor teoremini uygulayarak çözü­me gideriz.

Bu konuyla ilgili de soru çözelim. Aşağıdaki şekilde 45 derecelik açı verilmiş ve x uzunluğu sorulmaktadır.

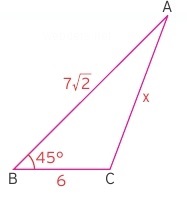
45 derecelik açıyı gördüğümüz için dikme inerek işlem yapmayı deneyelim.

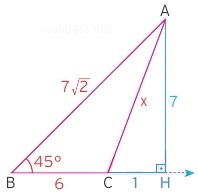
Dışarı indirilen dikme ile birlikte 45 - 45 - 90 üçgeni oluşmuştur. Bu durumda x üçgeni de Pisagor bağıntısı ile bulunur. 49 + 1 = 50, x = √50 bulunur.