Tam Sayılar Konu Anlatımı
Tam sayı, matematikteki en önemli kavramlardan biridir. Tam sayılar konusu ilk kez 6. sınıf ve 7. sınıf matematik derslerinde karşımıza çıkmaktadır. Bu yazıda tam sayılar nelerdir onu öğreneceğiz. Ardından da bazı örnekler çözeceğiz.
Matematiği öğrenmeye başladığımız zaman 0, 1, 2, 3 gibi sayılarla başlarız. Bu sayılar doğal sayılardır. Tam sayılar kümesi ise doğal sayıları kümesinden daha geniştir.
Tam sayıların ana özelliği virgüllü bir kısmının olmamasıdır. Örneğin 2,7 tam sayı değildir. Adından da anlaşılacağı gibi tam sayılar tam olmalıdır.
Tam Sayılar Hangileridir?
Yukarıda 0'dan 1, 2, 3 şeklinde devam ederek sonsuza kadar giden sayıların doğal sayılar olduğunu söyledik. Bu sayılara negatif olanları da eklersek eğer tam sayıları elde ederiz. Negatif sayılar 0'dan küçük sayılardır. Örneğin -3 bir negatif tam sayıdır. Buna karşın 3 pozitif tam sayıdır. Demek ki tam sayılar pozitif veya negatif olabilmektedir.
Peki, 0 tam sayı mıdır?
0 da tam sayıdır. Ancak 0 pozitif veya negatif değildir. 0 nötrdür. Yani işaretsizdir. Başında - ya da + bulunmaz. Normalde kullandığımız sayıların başında + vardır. Örneğin 8 dediğiniz zaman matematikte +8'i kast ederiz. Genellikle sadece negatif sayıların başına - konur. Pozitif sayıların başına günlük yazımda + işareti konmaz.
Tam sayılar kümesi kaçtan başlar diye bir soruyla karşılaşırsanız eksi sonsuzdan başlar artı sonsuza kadar devam eder diye cevap verebilirsiniz. Çünkü tam sayılar her iki taraftan da sonsuza gitmektedir. Bir başlangıç noktası ve ucu yoktur.
Sayı Doğrusunda Tam Sayılar
Sayı doğrusu matematikte sayıları gösterdiğimiz hayali bir doğrudur. İki ucunda ok vardır. Bu da sonsuza gittiği anlamına gelir. Yani sonsuza kadar bütün sayılar sayı doğrusunda bulunmaktadır.
Sayı doğrusunda tam sayılar olduğu gibi bu sayıların arasında tam olmayan kesirli ve ondalık sayılar da vardır. Burada bizim konumuz olan tam sayılardır.
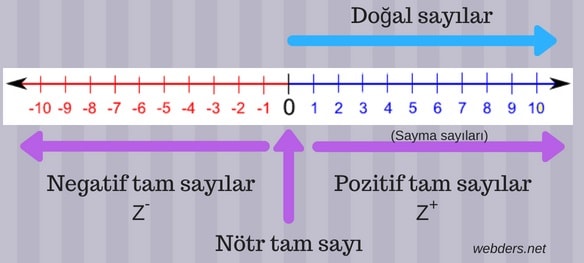
Yukarıdaki resimde tam sayıları, doğal sayıları ve sayma sayılarını görüyorsunuz. Pozitif tam sayılar Z+ ve negatif tam sayılar ise Z- ile gösterilir. Pozitif tam sayılara aynı zamanda sayma sayıları denir.
Sayı doğrusu üzerindeki sayıları iyi incelemek gerekir. Çünkü basit gelse de öğrenciler negatif sayıların nasıl büyüyüp küçüldüğünü karıştırmaktadır. Örneğin normalde 3 2'den büyükken -3 -2'den küçüktür. Çünkü sayı doğrusuna baktığınız zaman sola doğru sayıların küçüldüğünü, sağa doğru ise büyüdüğünü görürsünüz.
Tam sayılarda toplama ve çıkarma gibi işlemler yaparken karıştırmamak için pozitif tam sayıları elinizdeki para, negatif tam sayıları da elinizdeki borç gibi düşünebilirsiniz. Mesela 5 liranız varsa bu 3 liradan daha iyidir. Ancak 5 lira borcunuzun olması 3 lira borcunuzun olmasından kötüdür. Bu nedenle -5 -3'ten küçüktür.
Tam Sayılar ile İlgili Örnekler
Bir konuyu ne kadar iyi anlasak da konuyla ilgili örnekler çözmeden tam öğrenemeyiz. Bu nedenle test çözmek ders çalışma açısından çok önemlidir. Şimdi basit ama bilgileri pekiştirecek birkaç örnek yapalım.
- 4 - 2 = ?
- 1 - 9 = ?
- -3 - (-2) = ?
- 4 + (-7) = ?
- -2 x 12 = ?
- -4.-4 = ?
- -24 / -3 = ?
Cevaplar:
- 2
- -8
- -1
- -3
- -24
- 16
- 8
Tam sayılarda işlem yaparken toplama ve çıkarmada yukarıda örnek verdiğimiz para ve borç şeklinde düşünebilirsiniz. Çarpma ve bölmede ise şu kurallar geçerlidir:
- Aynı işaretli sayıların çarpılması veya bölünmesinde sonuç pozitif (+) olur.
- Zıt işaretli sayıların çarpılması veya bölünmesinde sonuç negatif (-) olur.
Örneğin negatif iki sayıyı çarparsanız da bölerseniz de sonuç pozitif olacaktır. Çünkü bu sayılar aynı işaretlidir. Sayılardan biri + diğeri - ise sonuç her zaman - çıkacaktır.
Etiketler:
Son Eklenenler
- Tarımla İlgili Meslekler
- Matematiği İyi Olmayanlar Hangi Mesleği Seçmeli?
- Antropoloji Nedir?
- Dünyanın Kaç Türlü Hareketi Vardır?
- Toplumsal Düzeni Sağlayan Kurallar Nelerdir?
- Cumhuriyet Yönetiminin Değerleri Nelerdir?
- İklim ve Hava Olayları Arasındaki Fark
- 1 Asal Sayı Mıdır?
- Homeostasi nedir?
- 2 ile Bölünebilme Kuralı
