Koni Formülleri

16.06.2018 - 20:04

Koni üç boyutlu ve sivri ilginç bir cisimdir. Üst üste küçülen daireler koyarsak koni elde ederiz. Koninin en üst kısmı bir nokta, en alt kısmı ise bir dairedir. Bu yazıda koni formülleri üzerinde kısaca duracağız.

Daha önce koninin hacmi ve yüzey alanı üzerinde durmuştuk.

Koni Açılımı ve Formülleri

Koninin formüllerine gelmeden önce koninin açılımını bilmemiz gerekir. Koniyi açtığımız zaman bir daire dilimi ve taban dairesini elde ederiz. Bu daire dilimini dairesel olarak sararsak koni elde ederiz.

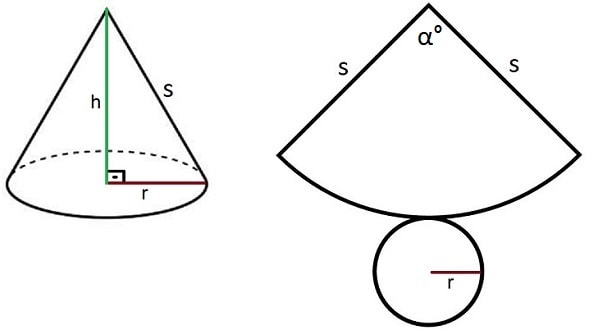
koni formülleri

Yukarıdaki şekilde koni açılımını görmekteyiz. Buradaki kavramları iyi öğrenirsek koni formüllerini çok daha iyi kavrarız. Görselde s harfiyle gösterilen uzunluk koninin ana doğrusudur. Koninin ana doğrusu açılımdaki daire diliminin de yarıçapı olmaktadır. Bu çok önemlidir. Aynı zamanda açılımdaki daire de koninin taban dairesidir.

Şimdi buna göre formülleri ortaya koyalım.

Formüller

Koninin taban alanı: A = π.r2.h

Koninin taban çevresi: Ç = 2.π.r

Koninin hacmi: Taban alanı x yükseklik / 3 ⇒ V = π.r2.h / 3

Koninin ana doğrusu ⇒ s2 = r2 + h2 (Pisagor bağıntısı ile ana doğru uzunluğu bulunabilir.)

Koni açı formülü: r / s = α / 360 (yarıçapın ana doğruya oranı, açılımdaki açının 360'a oranına eşittir.)

Koninin yüzey alanı: Açılımdaki daire ve daire diliminin alanını toplayarak bulabiliriz. Ya da π.r.(r + s) formülü kullanılabilir. İki durumda da aynı sonuç elde edilebilir.

Yukarıdaki açıklamalardan da anlaşılacağı üzere koninin açılımını anlamak formüllerini kavramak açısından çok önemlidir.

Son olarak konide taban çevresini açtığımız zaman ortaya çıkan daire diliminin dış tarafının uzunluğuna eşit olduğuna dikkat ediniz. Buradan da birçok şeyi elde edebilirsiniz.

Etiketler:
  • geometri    
    • Yorumlar
    Yorum Yap

    Son Eklenenler

    Son Etiketler

    2013 - 2022 © Webders.net