Koninin Hacmi ve Yüzey Alanı
Üç boyutlu geometrik cisimlerden biri konidir. Piramitler genel olarak tepe noktasına sahip üç boyutlu cisimler olarak sınıflandırılır.
Dairenin piramit haline koni denir. Bir daireyi düÅŸünün. Üstüne daha küçük bir daire eklediÄŸinizi düÅŸünün. Her seferinde daire alanını düzenli bir ÅŸekilde küçülterek üst üste eklediÄŸinizde en üst daire noktasal olur. Ortaya çıkan geometrik ÅŸekil de konidir.
Günlük hayatta koniye çeÅŸitli yerlerde rastlarız. ÖrneÄŸin yılbaÅŸlarında takılan sivri ÅŸapka bir konidir. Ya da içine patlamış mısır, ay çekirdeÄŸi konan sivri kâğıt kap yine bir koni örneÄŸidir.
Yukarıdaki resimde bir koni örneÄŸi gösterilmiÅŸtir.
Koninin Hacmi
Koninin hacmi genel olarak piramidin hacmi nasıl bulunursa öyle bulunur. Yani tam bir ÅŸekil gibi hacim hesaplanır ve 3’e bölünür.
EÄŸer konide daralma olmasaydı bir silindir elde edilecekti. Öyleyse koni aynı yükseklikte ve aynı taban alanına sahip bir silindirin 3’te biri kadar bir hacme sahiptir.
Konin hacmi V = 1/3.π × r2 × h formülüyle bulunur.
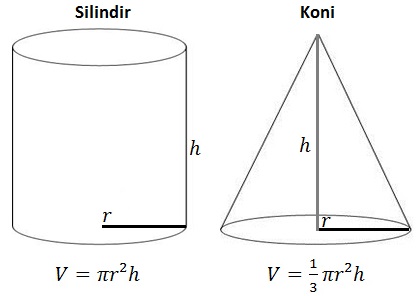
Yukarıdaki görselde koni ve silindirin hacimleri arasındaki iliÅŸki gösterilmiÅŸtir. Koninin hacminin silindirin hacminin 3’te 1’i kadar olduÄŸuna dikkat ediniz. Piramitlerde genel olarak bu iliÅŸki vardır.
Koniyle ilgili hacim sorularında silindir gibi düÅŸünüp üçe bölmek en kolay yöntemdir. Silindirin hacmi ve yüzey alanı ile ilgili yazıda silindir ile ilgili bilmemiz gerekenleri anlatmıştık.
Koninin Yüzey Alanı
Koninin hacmi kolay bulanabiliyor ancak öÄŸrenciler koninin yüzey alanı nasıl bulunur pek bilmiyor. Konide zorlanma genellikle yüzey alanıyla ilgili oluyor.
Konide yüzey alanı bulmak için konideki temel uzunlukları bilmemiz gerekir. Bu uzunluklardan biri yarıçap, diÄŸeri yükseklik, bir diÄŸeri ise yanal uzunluktur.
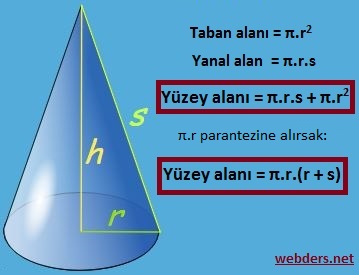
Yukarıdaki resimde koninin temel uzunlukları ve yüzey alanı gösterilmiÅŸtir. Åžimdi bunun üzerinden formülü açıklamaya çalışalım.
Koninin açılımdan yarıçapı s olan bir yay dilimi ve yarıçapı r ola bir tam daire elde edilecektir. Koninin yüzey alanı bu ikisinin toplamıdır.
Taban alanın nasıl bulunduÄŸunu hepimiz biliyoruz. BildiÄŸimiz dairenin alanı formülü ile bulunur. Yanal alan ise π.r.s formülüyle bulunur.
Öyleyse iki alanı topladığımızda yüzey alanı = π.r.(r + s) elde edilecektir.
Koninin Kesit Alanı
Koninin kesit alanı için de aynı ÅŸekilde pratik bilgimizi kullanmamız gerekir. Koninin üst üste daralarak eklenen dairelerden oluÅŸtuÄŸunu biliiyoruz. Öyleyse koni ÅŸapkasını da herhangi bir noktadan kesersek ortaya yine bir daire çıkacaktır.
Bunun için ekstra bir formül ortaya çıkarmaya gerek yoktur. Pisagor bağıntısı ve benzeri geometri bilgilerini kullanarak kesin alanı oluÅŸturan dairenin yarıçapını bulmaya çalışmalıyız. Bunu bulduktan sonra da normal daire alanı formülüyle sonuca ulaÅŸabiliriz.
Åžimdi de birkaç örnek soru çözerek konuyu pekiÅŸtirmeye çalışalım.
Örnek Sorular
AÅŸağıdaki soruları yukarıda anlatılanlar çerçevesinde çözmeye çalışın.
Soru: Yarıçap uzunluÄŸu 2, yüksekliÄŸi 8 cm olan bir koninin hacmi kaç cm3 olur? (π = 3)
A) 24
B) 32
C) 48
D) 60
E) 64
Çözüm: Formülü uyguladığımız zaman 1/3.3.22.8 = 32 cm3 bulunur. Cevap B seçeneÄŸidir.
Soru: Yarıçapı 7, yüksekliÄŸi 24 cm olan bir koninin yüzey alanı kaç cm2 olur? (π = 3)
A) 168
B) 322
C) 400
D) 568
E) 672
Çözüm: Formülü uygulamak için yanal uzunluÄŸa ihtiyacımız vardır. Pisagor bağıntısı uygularsak (7, 24, 25 üçgeni) yanal uzunluk s = 25 cm bulunur. Åžimdi formülü yerine koyalım.
π.r.(r + s) için 3.7.(7 + 25) = 672 cm2 bulunur. DoÄŸru yanıt E seçeneÄŸidir.
Etiketler:
Son Eklenenler
- Tarımla İlgili Meslekler
- Matematiği İyi Olmayanlar Hangi Mesleği Seçmeli?
- Antropoloji Nedir?
- Dünyanın Kaç Türlü Hareketi Vardır?
- Toplumsal Düzeni Sağlayan Kurallar Nelerdir?
- Cumhuriyet Yönetiminin Değerleri Nelerdir?
- İklim ve Hava Olayları Arasındaki Fark
- 1 Asal Sayı Mıdır?
- Homeostasi nedir?
- 2 ile Bölünebilme Kuralı