In Fonksiyonu ve Özellikleri
Matematikte birçok özel tanımlı fonksiyon vardır. Fonksiyonları iyi kavramak için önemli fonksiyonların karakterini bilmemiz gerekir. Bir fonksiyonun karakterini anlamak için grafiğini incelemek lazımdır. Ya da karakterini bildiğimiz bir fonksiyonun grafiğini daha rahat elde edebiliriz.
Bu yazıda matematikte çok önemli bir yeri olan In fonksiyonu üzerinde duracağız. Öncelikle şunu unutmayalım ki ln fonksiyonu bir logaritma fonksiyonudur. Logaritma için geçerli bütün özellikler ln fonksiyonu için de geçerlidir. Bu fonksiyonu doğal logaritma olarak tanımlamaktayız. Çünkü ln’in tabanı olan “e sayısı” matematikte bir sürü sahada karşımıza çıkan ve seri ile elde edilen doğal bir sayıdır. Bu nedenle e sayısı logaritmada bazı benzersiz özellikler taşır.
In Fonksiyonun Grafiği
Bildiğimiz gibi logaritmanın veya tabanı 0 olamaz. Bu durumlarda logaritma tanımsız olur. Tabanı e olan ln fonksiyonu da aynı özellikleri gösterir. İçi 1 olduğunda 0 değerini verir. Ancak tanım aralığı 0 olamaz. Fonksiyon grafiği negatif taraftan sert bir şekilde gelip pozitif tarafta x eksenine yakın bir seyirle artarak devam eder.
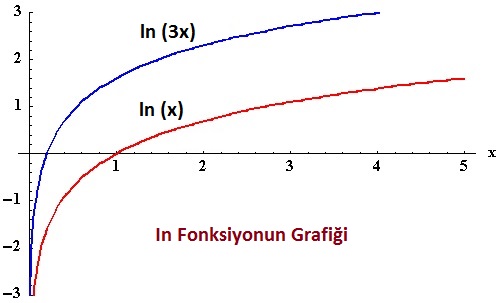
Yukarıdaki grafikte lnx ve ln3x değerleri verilerek karşılaştırma olanağı sağlanmıştır.
Bazı Pratik Özellikler
Logaritmanın özellikleri aynen ln için de geçerlidir dedik. Bu özelliklerden en çok işimize yarayacak olanları görelim.
- Çarpma kuralı: ln(x ∙ y) = ln(x) + ln(y)
- Bölme kuralı: ln(x / y) = ln(x) - ln(y)
- Üst kuralı: ln(x y) = y ∙ ln(x)
- In1 = 0
Yukarıdaki üç özelliği logaritmada çok iyi bilmemiz gerekir.
- In türevi: f (x) = ln(x) ⇒ f ' (x) = 1 / x
- In integrali: ∫ ln(x)dx = x ∙ (ln(x) - 1) + C
- Lim(ln(x)) [x⇒ 0] = -∞
Görüldüğü gibi ln logaritmasının limit, türev ve integral konuları açısından da özellikleri vardır. Özellikle ln’in türevi çok iyi bilinmelidir.
Etiketler:
Son Eklenenler
- Tarımla İlgili Meslekler
- Matematiği İyi Olmayanlar Hangi Mesleği Seçmeli?
- Antropoloji Nedir?
- Dünyanın Kaç Türlü Hareketi Vardır?
- Toplumsal Düzeni Sağlayan Kurallar Nelerdir?
- Cumhuriyet Yönetiminin Değerleri Nelerdir?
- İklim ve Hava Olayları Arasındaki Fark
- 1 Asal Sayı Mıdır?
- Homeostasi nedir?
- 2 ile Bölünebilme Kuralı
