Çeşitkenar Üçgen
Üçgenleri sınıflandırırken çeÅŸitkenar üçgen karşımıza bir üçgen türü olarak çıkar. Aslında çeÅŸitkenar üçgen özel bir üçgen deÄŸildir. Üçgen çeÅŸitleri konusuna bakan birisi bunu görebilir. Üçgenleri açı ölçülerine veya kenar uzunluklarına göre sınıflandırabilmekteyiz. Her iki sınıflandırma içerisinde de çeÅŸitkenar üçgenin yerini bulması mümkün. Bir üçgenin üç kenarının üçü de farklı uzunluktaysa bu üçgen bir çeÅŸitkenar üçgendir. ÇeÅŸitkenar üçgende açıların farklı olmasının sonucu olarak kenarlar da farklı olacaktır. Üçgende açılar konusunu iyi anlarsak çeÅŸitkenar üçgen dediÄŸimiz üçgenin hiçbir eÅŸitliÄŸe dayanmadan rastgele çizdiÄŸimizin bir üçgen olduÄŸunu görürüz. Şöyle ki, göz kararıyla çizdiÄŸimiz bu üçgende eÅŸitlik olması pek olası deÄŸildir. Bu nedenle çeÅŸitkenar üçgeni rastgele üçgen olarak da ifade edebiliriz.
Özel üçgenler içerisinde çeÅŸitli yöntemlerle uzunluk ve alan hesabı yapabiliyorduk. Ancak çeÅŸitkenar üçgende üçgenin çevresi veya alanı için çok özel yöntemlerimiz olmayabiliyor. Bu durumu açıklamak için bir çeÅŸitkenar üçgen üzerinden gösterim yapalım.
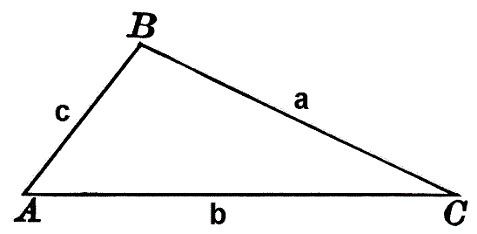
Yukarıdaki üçgen örnek bir çeÅŸitkenar üçgendir. KöÅŸeler büyük harfle gösterilmiÅŸ, kenarlar ise o köÅŸelere denk gelecek ÅŸekilde küçük harfle ifade edilmiÅŸtir.
ÇeÅŸitkenar Üçgenin Çevresi
ÇeÅŸitkenar üçgenin çevresi diÄŸer üçgenlerde olduÄŸu gibi kenarların toplamı ile bulunur. Yani çevre = a + b + c olur. EÄŸer bilinmeyen bir kenar varsa ve açı biliniyorsa bulun için kosinüs teoremi kullanılır.
Bunun dışında çeÅŸitkenar üçgende çevre hesabı ile ilgili yapabilecek pek bir ÅŸey yoktur. Kosinüs teoremi için ise en az iki kenar ve bir özel açı verilmesi gerekir. Özel açı verildikten sonra isteyen kosinüs teorimi yerine dikme indirerek de üçüncü kenara ulaÅŸabilir.
ÇeÅŸitkenar Üçgenin Alanı
ÇeÅŸitkenar üçgenin alanı hesaplanırken eÄŸer özel bir açı ve o açının iki yanındaki kenar uzunlukları biliniyorsa sinüs teoremi çok iyi bir yöntem olacaktır. Sinüslü alan formülü de denen bu yönteme göre iki kenarın uzunluÄŸu ile aradaki açının sinüsünün yarısı o üçgenin alanını verecektir. Bir de burada çeÅŸitkenar üçgenin alanı için baÅŸka bir formül de vardır. Bu formül çok karşımıza çıkmasa da bazı yerlerde faydalı olmaktadır. Hatta bazı alan soruları sadece bu formülle çözülebilmektedir.
ABC üçgenin kenarları a, b ve c ile gösterilmiÅŸ olsun. Bu durumda alan için önce u = (a + b + c)/2 olmak üzere Alan =√[ u(u-a)(u-b)(u-c)] olacaktır. EÄŸer sayılar uygun verilmiÅŸse bu yöntemle gayet güzel sonuçlar elde edebiliriz.
Mesela kenarları 5, 6 ve 7 birim olan bir üçgenle ile ilgili baÅŸka bir bilgimiz olmasın. Bizden alan istendiÄŸinde önce u = (5 + 6 + 7)/2 = 9 olur. Bu durumda alan =√ 9(9-5)(9-6)(9-7) olacaktır. Bu da 6√6 sonucunu verecektir.
Etiketler:
Son Eklenenler
- Tarımla İlgili Meslekler
- Matematiği İyi Olmayanlar Hangi Mesleği Seçmeli?
- Antropoloji Nedir?
- Dünyanın Kaç Türlü Hareketi Vardır?
- Toplumsal Düzeni Sağlayan Kurallar Nelerdir?
- Cumhuriyet Yönetiminin Değerleri Nelerdir?
- İklim ve Hava Olayları Arasındaki Fark
- 1 Asal Sayı Mıdır?
- Homeostasi nedir?
- 2 ile Bölünebilme Kuralı
