Polinomlar Konu Anlatımı

Polinomlar konusu matematik için önemli bir konudur. Bu ders notunda polinomlar üzerinde duracağız ve nedir ne değildir öğrenmeye çalışacağız.

n doğal sayı a₀, a₁, a₂, .... , a_n gerçel sayılar ve x değişken olmak üzere,

P(x) = a₀ + a₁x + a₂x² + .... + a_nxⁿ şeklinde tanımlanan ifadelere gerçel katsayılı bir bilinmeyenli polinom denir.

• P(x) polinomunda a₀, a₁, a₂, .... , a_n gerçel sayılarına polinom katsayıları denir.
• P(x) polinomunda a₀ + a₁x + a₂x² + .... + a_nxⁿ ifadelerine polinom terimleri denir.
• P(x) polinomunda derecesi en büyük olan terimin katsayısına polinom baş katsayısı denir.
• P(x) polinomunda x' in en büyük kuvveti olan doğal sayıya P(x) polinomunun derecesi denir ve der (P(x)) ile gösterilir.
• Tüm katsayıları sıfır olan polinoma sıfır polinomu denir.

• P(x) = a₀ + a₁x + a₂x² + .... + a_nxⁿ polinomunda a₀ ≠ 0, a₁ = a₂ = ..... = a_n = 0 ise P(x) polinomuna sabit polinom denir ve P(x) = a₀ şeklinde gösterilir.

İki değişkenli Polinomlar

Katsayıları reel sayı, x ve y değişkenlerinin kuvvetlerinin kuvvetleri doğal sayı olmak üzere, P(x, y) şeklindeki polinomlara iki değişkenli polinom denir.

Örnek: P(x, y) = 2xy² - 3x²y³ + 4

olduğuna göre P(1, -1) kaçtır?

Çözüm:

P(x, y) = 2xy² - 3x²y³ + 4

P(1, -1) = 2.1.(-1)² - 3.1².(-1)³ + 4

= 2 + 3 + 4

= 9

Örnek: P(x, y) = x⁴y³ - 2x⁵ + y⁶ -3x⁵y⁴

olduğuna göre P(x, y) polinomunun derecesi kaçtır?

Çözüm: P(x, y) polinomunun derecesi a.xⁿ.yⁿ terimindeki n + m toplamının en büyük olanıdır.

3x⁵.y⁴ teriminde 5 + 4 = 9 toplamı en büyük olduğundan polinomun derecesi 9 dur.

İki Polinomun Eşitliği

İki polinomun eşit olabilmesi için dereceleri aynı olan terimlerin katsayıları da aynı olmalıdır.

P(x) = a₀ + a₁x + a₂x² + ..... + a_nxⁿ

Q(x) = b₀ + b₁x + b₂x² + ..... + b_nxⁿ

polinomlarında P(x) = Q(x) olabilmesi için

a₀ = b₀, a₁ = b₁, a₂ = b₂, a_n = b_n

olmalıdır.

Örnek:

(a - 1)x³ + 4x² + c + 2 = 3x³ + (b - 1)x2 + (2 - d)x

olduğuna göre a + b + c + d toplamı kaçtır?

Çözüm:

Aynı dereceli terimlerin katsayıları eşit olmalıdır.

Yani;

a -1 = 3, b - 1 = 4, 2 - d = 0, c + 2 = 0

a = 4, b = 5, d = 2, c = -2

O halde, a + b + c + d = 4 + 5 - 2 + 2 = 9

Örnek:

P(x) = (2x - 3)(x + a)

Q(x) = 2x² - x + b

P(x) = Q(x) olduğuna göre, a.b çarpımı kaçtır?

Çözüm:

P(x) = Q(x)

(2x - 3)(x + a) = 2x² - x + b

2x² + x(2a - 3) - 3a = 2x² - x +b

Aynı dereceli terimlerin katsayıları eşit olmalıdır.

2a - 3 = -1 , b = -3a

a = 1 b = -3

O halde; a.b = 1.(-3) = -3 tür.

Örnek:

P(x) = x² + nx - 5

Q(x) = 9x + m

P(3x - 1) = Q(x² - x)

olduğuna göre m - 2n farkı kaçtır ?

Çözüm:

P(3x - 1) = Q(x² - x) eşitliğinde x yerine 1 yazalım

P(2) = Q(0)

2² + 2n - 5 = 9.0 +m

m - 2n = -1

Polinomlarda Toplama ve Çıkarma İşlemi

İki polinom arasında toplama veya çıkarma işlemi yapılırken, aynı dereceden terimlerin katsayıları toplanır veya çıkarılır.

a.xⁿ + b.xⁿ = (a + b).xⁿ

a.xⁿ - b.xⁿ = (a - b).xⁿ

Örnek:

P(x) = x³ - 3x² + 5x + 1

Q(x) = x² + 4x + 4

olduğuna göre P(x) - Q(x) fark polinomu aşağıdakilerden hangisidir ?

A) x³ + 4x² - 5x + 1 B) x³ + x² - x -3 C) x³ + 4x² - x +5

D) x³ - 4x² + x -5 E) x³ - 4x² + x -1

Çözüm:

P(x) - Q(x) = (x³ - 3x² + 5x - 1) - (x² + 4x + 4)

= x³ - 3x² + 5x - 1 - x² - 4x - 4

= x³ - 4x² + x + 5 (Cevap : D)

Örnek:

P(x) + P(x + 2) = 4x + 2

olduğuna göre P(-2) kaçtır ?

Çözüm:

I. dereceden iki polinomun toplamı birinci dereceden bir polinom olduğuna göre P(x) = ax + b olmalıdır.

P(x) + P(x + 2) = 4x + 2

ax + b + a(x + 2) + b = 4x + 2

ax + b + ax + 2a + b = 4x + 2

2ax + 2a + 2b = 4x + 2

İki polinomun eşitliğinden ,

2a = 4 ve 2a + 2b = 2

a =2 4 + 2b = 2

b = -1

Buna göre; P(x) = ax + b = 2x - 1 dir.

x = -2 için P(-2) = 2.(-2) - 1

= -5 tir.

Polinomlarda Çarpma işlemi

P(x) ve Q(x) polinomları çarpılırken I. polinomun her bir terimi II. polinomun her bir terimi ayrı ayrı çarpılarak toplanır.

Örnek:

P(x) = x³ - 4x + 1

Q(x) = x² + x

H(x) = P(x).Q(x)

olduğuna göre H(1) değeri kaça eşittir ?

Çözüm:

I. Yol:

H(1) = P(1). Q(1) olduğuna göre

P(1) = 1³ - 4.1 + 1 = -2

Q(1) = 1² + 1 = 2

H(1) = P(1). Q(1) = 2.(-2) = -4 tür.

II. Yol:

H(x)= P(x). Q(x)

H(x) = (x³ - 4x +1). (x² + x)

H(x) = x⁵ + x⁴ - 4x³ - 4x² + x² + x

H(x) = x⁵ + x⁴ - 4x³ - 3x² + x

H(1) = 1⁵ + 1⁴ - 4.1³ - 3.1² + 1

H(1) = 1 + 1 - 4 - 3 + 1 = -4 tür.

Örnek:

P(x) = 2x³ - 3x + 1

Q(x) = x⁴ - 5x² + 3

olduğuna göre, [P(x²)].[Q(x³)]² çarpım polinomunun derecesi kaçtır ?

Çözüm:

Bir polinomun derecesi bulunurken en büyük dereceli terimler alınarak işlem yapılır.

P(x) polinomunun derecesi 3 olduğundan P(x) = x³

Q(x) polinomunun derecesi 4 olduğundan Q(x) = x⁴

alınabilir.

O halde; P(x²).[Q(x³)]² = (x²)³.[(x⁴)³]²

= x⁶.x²⁴

= x³⁰

olduğuna göre bu polinomun derecesi 30 dur.

Örnek:

ax³ + bx² + cx + d = (x - 3).(x² + 2x - 1)

olduğuna göre, b - c - a + d ifadesinin değeri kaçtır ?

Çözüm:

ax³ + bx² + cx + d = (x - 3).(x² + 2x + 1)

eşitliğinde x = -1 yazalım.

-a + b - c + d = (-1 -3).(1 -2 -1)

b - c - a + d = (-4).(-2)

= 8 dir.

Örnek:

P(x) = 2x³ - x² + 2x -5

olduğuna göre, P(x - 2) polinomunun katsayılar toplamı kaçtır ?

Çözüm:

P(x - 2) polinomunun katsayılar toplamı sorulduğundan x = 1 değerini bu polinomda yerine yazalım.

x = 1 için P(1 - 2) = P(-1) in değerini bulmalıyız.

P(x) = 2x³ - x² + 2x - 5 ifadesinde P(-1) i bulmak için x = -1 yazalım.

x = -1 için P(-1) = 2.(-1)³ - (-1)² + 2(-1) - 5

= -10

Örnek:

P(x + 2) = x² + 4x -5

olduğuna göre, P(3x - 2) polinomunun ssabit terimi kaçtır ?

Çözüm:

P(3x - 2) polinomunun sabit terimi, x = 0 için P(-2) dir.

P(x + 2) = x² + 4x - 5 ifadesinde P(-2) yi bulmak için x = -4 yazalım.

x = -4 için P(-2) = (-4)² + 4(-4) - 5

= -5 tir.

Polinomlarda Bölme İşlemi

Polinomlarda bölme işlemi ile ilgili birçok soru gelmektedir. Özellikle kalan bulma soruları polinomlar konusundan en çok soru gelen yerdir.

der(P(x)) ≥ der(Q(x)) ve Q(x) ≠ 0 olmak üzere, P(x) polinomunun Q(x) ile bölümünde bölüm B(x), kalan K(x) olsun.

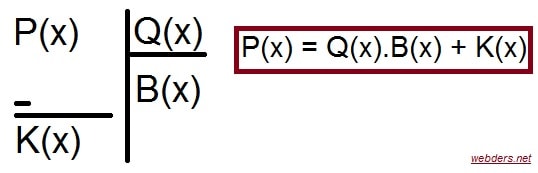
Polinomlardan gelen soruları çözebilmek için yukarıdaki bağıntının çok iyi öğrenilmesi gerekir.

Örnek:

P(x) = 3x³ - 2x² + 5

polinomunun (x - 1) ile bölümünden kalan kaçtır ?

Çözüm:

P(x) polinomunun (x - 1) ile bölümünden bölüm B(x), kalan K ise

3x³ - 2x² + 5 = (x - 1).B(x) + K

x = 1 için 3.1³ - 2.1² + 5 = (1 - 1).B(1) + K

3 - 2 + 5 = K

K = 6 dır.

Örnek:

P(x) = x² + x + n

polinomunun (x + 3) ile bölümünden kalan 5 olduğuna göre, n kaçtır ?

Çözüm:

P(x) polinomunun (x + 3) ile bölümünden kalan 5 ise P(-3) = 5 tir.

x = -3 için P(-3) = (-3)² + (-3) + n

5 = 6 + n

n = -1

Örnekler:

• P(x) polinomunun (6x - 3) ile bölümünden kalan 2 ise, P(½ ) = 2 dir.
• P(x + 3) polinomunun (x - 4) ile bölümünden kalan 4 ise, P(7) = 4 tür.
• P(4x - 2) polinomunun sabit terimi -5 ise, P(-2) = -5 tir. (Sabit terim için x yerine 0 yazılır).
• P(5x - 3) polinomunun katsayılar toplamı 6 ise, P(2) = 6 dır. (Katsayılar toplamı için x yerine 1 yazılır.)
• (x - 3).P(x) + x3.Q(x) polinomunun x - 1 ile bölümünden kalan 8 ise, (1 - 3).P(1) + 1.Q(1) = 8 ve -2.P(1) + Q(1) = 8 dir.

Örnek:

P(x - 2) polinomunun (x + 1) ile bölümünden kalan 3, Q(x + 2) polinomunun (x - 1) ile bölümünden kalan 5 tir.

Buna göre, P(x - 6) + Q(x) polinomunun (x - 3) ile bölümünden kalan kaçtır ?

Çözüm:

P(x - 2) polinomunun (x + 1) ile bölümünden kalan 3 ise, P(-3) = 3 tür.

Q(x + 2) polinomunun (x - 1) ile bölümünden kalan,

P(3 - 6) + Q(3) = P(-3) + Q(3)

= 3 + 5

= 8 dir.

Örnek:

P(x) = x³ - x² - 2x - 1

polinomunun (x² - x + 2) ile bölümünden kalan aşağıdakilerden hangisidir ?

A) 2x - 1 B) -4x - 1 C) 4x + 1 D) x + 4 E) x - 4

Çözüm:

P(x) polinomunun (x² - x + 2) ile bölümünden kalan bulmak için ( x² - x + 2 = 0 ise x² = x - 2 olduğundan ) P(x) polinomunda x² yerine (x - 2) yazalım.

P(x) = x².x - x² - 2x - 1

K(x) = x(x - 2) - (x - 2) - 2x - 1

= x² - 2x - x + 2 - 2x - 1

= x - 2 - 5x + 1

= -4x - 1 dir. (Cevap: B)

P(x) polinomunun (x - a)² ile tam bölünebilmesi için; P(a) = 0 ve P'(a) = 0 olmalıdır. (P'(x) ifadesi P(x) polinomunun birinci dereceden türevidir.)