İki Noktası Bilinen Doğrunun Denklemi
İki noktası bilinen doğrunun denklemi analitik geometrinin en önemli konularından biridir. Doğru denklemi yazmak istiyorsak önce bir doğru denklemi için neye ihtiyaç olduğunu bilmemiz gerekir. Bir doğrunun denklemini yazabilmek için iki şeye ihtiyaç vardır:
- Doğrunun eğimi
- Doğru üzerindeki herhangi bir noktanın koordinatları
Dolayısıyla eğimi ve bir noktası bilinen doğru denklemi ekstra hiçbir bilgiye ihtiyaç duymadan yazılabilir. Daha önce bu konuyu işledik: Bir noktası ve eğimi bilinen doğru denklemi
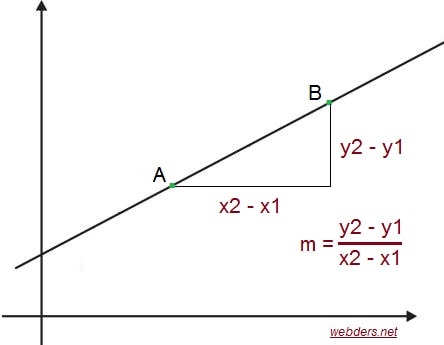
Eğer elimizde iki nokta varsa şöyle bir yöntem uygularız. Önce iki noktadan doğrunun eğimini buluruz. Ardından da eğim ve harhengi bir noktayla denklemi yazarız.
İki Noktadan Eğimin Bulunması
İki noktadan doğru eğimini bulurken y'ler farkını x'ler farkına böleriz. Eğime m dersek m = (y2 - y1) / (x2 - x1) olur.
Bir örnek yapalım. A(1, 4) ve B(3, 10) noktasından geçen doğrunun eğimini bulalım. Formülü uygularsak m = (10 - 4) / (3 - 1) = 6 / 2 = 3 bulunur.
İki noktadan yalnız bir doğru geçtiği için iki noktadan geçen doğrunun eğimi de tektir. Burada önemli olan y'ler farkının x'ler farkına bölünmesidir. Örnekte biz B noktasından A noktasını çıkarıp böldük. Ancak bunun tersini yapsak da sonuç değişmeyecektir.
Bir örnek daha yapalım. K(-1, 3) ve L(2, 6) noktasından geçen doğrunun eğimini bulalım. Yine ordinatlar farkını apsisler farkına böleceğiz. Yani m = (6 - 3) / (2 - -1) = 3 / 3 = 1 bulunur.
Denklemin Yazılması
Denklemi yazmak için eğime ve bir noktaya ihtiyaç olduğunu söyledik. İki noktası bilinen doğrunun eğimi bulduktan sonra geriye kalan denklemi yazmaktır. Yapmamız gereken tek şey eğim ile noktaları eşitleyip denklem kurmaktır.
Doğru üzerindeki noktanın koordinatlarına (a, b) dersek denklemimiz y - b = m(x - a) olur. Ardından istediğimiz düzenlemeleri yapıp denkleme son şeklini verebiliriz.
Örneğin eğimi 5 olan ve L(1, 2) noktasından geçen doğrunun denklemi y - 2 = 5.(x - 1) olur. Bunu da açtığımız zaman y - 2 = 5x - 5 ⇒ y = 5x - 3 doğrusu elde edilir.
Şimdi de iki noktası bilinen doğrunun eğimini bulup denklemini yazmayı deneyelim.
Soru: Düzlemde A(1, 4) ve B(2, 6) noktalarından geçen doğrunun denklemini yazınız.
Çözüm: Yukarıda da belirttiğimiz gibi önce eğimi bulmalıyız. Eğimi bulmak için y'ler farkını x'ler farkına bölelim. 6 - 4 = 2, 2 - 1 = 1 ⇒ m = 2/1 = 2 olur.
Şimdi denklem için elimizde eğim var. Geriye kalan noktalardan birini kullanmaktır. Doğru üzerinde iki nokta biliyoruz. Herhangi birini kullanabiliriz. İkisinde de sonuç aynı çıkacaktır. Örneğin 1, 4 noktasını seçelim.
Bu durumda denklem y - 4 = 2.(x - 1) ⇒ y - 4 = 2x - 2 ;⇒ y = 2x + 2 şeklinde denklem bulunur. Dilersek denklemin doğru olup olmadığını anlamak için iki noktayı da denklemde yerine koyarız. Eğer denklemler şartı sağlıyorsa bu durumda denklem doğru demektir.
Etiketler:
Son Eklenenler
- Tarımla İlgili Meslekler
- Matematiği İyi Olmayanlar Hangi Mesleği Seçmeli?
- Antropoloji Nedir?
- Dünyanın Kaç Türlü Hareketi Vardır?
- Toplumsal Düzeni Sağlayan Kurallar Nelerdir?
- Cumhuriyet Yönetiminin Değerleri Nelerdir?
- İklim ve Hava Olayları Arasındaki Fark
- 1 Asal Sayı Mıdır?
- Homeostasi nedir?
- 2 ile Bölünebilme Kuralı
