Dikdörtgenin Alanı ve Çevresi
Günlük hayatta ne çok kullandığımız geometrik şekil dikdörtgendir. Dikdörtgen konu anlatımı kısmında dikdörtgen ile ilgili önemli şeyleri anlatmıştık. 3. sınıftan itibaren dikdörtgenin alanı ve çevresi ile ilgili sorularla karşılaşırız. Şimdi dikdörtgenin alanı ve çevresi ile ilgili bilgi verelim.
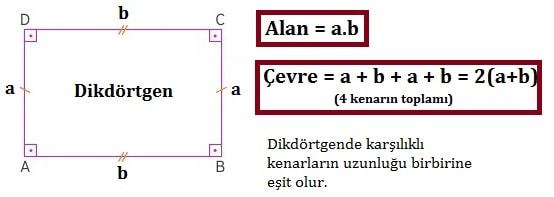
Dikdörtgenin temel özelliği dörtgen olması ve 4 kenarının da birbirine dik olmasıdır. Bunun sonucu olarak karşılıklı kanarlar eşit uzunlukta ve paralel olmaktadır. Dikdörtgenin kısa kenarına a, uzun kenarına b dersek;
- Dikdörtgenin alanı formülü A = a.b olur.
- Dikdörtgenin çevresi formülü Ç = 2(a + b) olur.
Bu iki formülü de sürekli kullanırız.
Dikdörtgen Kare ve Palelkenar İlişkisi
Dikdörtgen kare ve paralelkenar gibi dörtgenlerin hepsi özel dörtgenler sınıfına girmektedir. Paralelkenarda görülen ilk özellik karşılıklı kenarların paralel olmasıdır. Bu da karşılıklı kenar uzunluklarının eşit olması anlamına gelmektedir.
Paralelkenardan daha özel olan dörtgen dikdörtgendir. Burada ekstradan kenarların dik olması da söz konusu olmaktadır.
Dikdörtgendeki uzun kenar ile kısa kenarın uzunluğu eşit olduğunda bu sefer kare ortaya çıkar. Yani a ve b kenarlı yerine bütün kenarlar a olur. Kare dikdörtgenin daha özel hale gelmiş versiyonudur. Kare bir düzgün çokgendir çünkü bütün kenar uzunlukları eşittir.
Karenin özellikleri yazısında belirttiğimiz özelliklerden bazıları dikdörtgen için de geçerliyken bazıları geçerli değildir. Örneğin karede köşegenler mutlaka dik kesişir. Ancak dikdörtgende köşegenler dik kesişmez.
Karenin çevresi 4a, alanı ise a2 olur. Çünkü dikdörtgendeki gibi uzun ve kısa kenarı yoktur. 4 kenarın da uzunluğu aynıdır.
Dikdörtgenin Özellikleri
Dikdörtgenin özellikleri maddeler halinde şöyle sıralanabilir:
- Dört kenarı olan bir çokgendir yani dörtgendir.
- Kenarları birbirine diktir.
- Karşılıklı kenarlar paraleldir ve karşı kenarlarının uzunlukları birbirine eşittir.
- Dört iç açısı da 90° derecedir. Böylece iç açıları toplamı 360°'dir.
- İki adet köşegeni vardır.
- Köşegenler birbirini ortalar ve ağırlık merkezinde kesişir.
- İki köşegen çizildiğinde 4 adet ikizkenar üçgen ortaya çıkar.
- Çevresi 2(a + b) ve alanı a.b şeklinde bulunur.
Dikdörtgenin Alanı ve Çevresi ile İlgili Çözümlü Sorular
Yukarıda dikdörtgen için ala ve çevre formüllerini verdik. Ancak konuyla ilgili sorulan sorular her zaman çok basit olmamaktadır. Örneğin alanı verilen bir dikdörtgenin çevresini bulma ya da çevresi verilen dikdörtgenin alanını bulma gibi sorular karşımıza sık çıkmaktadır. Bu durumda biraz da matematik bilgimizi kullanarak soruları çözebiliriz.
Soru: Uzun kenarı kısa kenarının 2 katı olan ve çevresi 24 cm olan dikdörtgenin alanı kaç cm2 olur?
A) 24
B) 28
C) 32
D) 36
E) 40
Çözüm: Çevre formülü 2(a + b) şeklindedir. Kısa kenar a, uzun kenar b şeklinde düşünülürse b = 2a olur. Öyleyse b yerine formülde 2a yazabiliriz.
2(a + 2a) = 24 ⇒ 2.3a = 24 ⇒ 6a = 24 ⇒ a = 4 cm bulunur. Öyleyse b kenarı da 8 cm olur. Alan = a.b olduğundan, 4.8 = 32 cm2 bulunur. Cevap C seçeneğidir.
Soru: Kenar uzunlukları birbirinden farklı ve a, b şeklinde doğal sayılar olan bir dikdörtgenin alanı 36 cm2'dir. Buna göre bu dikdörtgenin çevresinin en küçük değeri kaç cm olur?
A) 18
B) 20
C) 22
D) 24
E) 26
Çözüm: Soruda alan verilmiş ve çevrenin en küçük değeri sorulmaktadır. Çevrenin en küçük değeri alması için a ve b uzunluklarının birbirine yakın olması gerekir.
Alandan bildiğimize göre a.b = 36'dır. Öyleyse a ve b'nin alabileceği doğal sayı değerleri şunlardır:
- 36, 1
- 18, 2
- 12, 3
- 9, 4
- 6, 6
Bu değerler içerisinde birbirine en yakın olan 6 ile 6'dır. Ancak soruda bize kenar uzunlukları birbirinden farklı denmiştir. O zaman en yakın değerler olarak 9 ile 4'ü alırız. Bu durumda 2.(9 + 4) = 2.13 = 26 cm olur. Cevap E seçeneğidir.
Etiketler:
Son Eklenenler
- Tarımla İlgili Meslekler
- Matematiği İyi Olmayanlar Hangi Mesleği Seçmeli?
- Antropoloji Nedir?
- Dünyanın Kaç Türlü Hareketi Vardır?
- Toplumsal Düzeni Sağlayan Kurallar Nelerdir?
- Cumhuriyet Yönetiminin Değerleri Nelerdir?
- İklim ve Hava Olayları Arasındaki Fark
- 1 Asal Sayı Mıdır?
- Homeostasi nedir?
- 2 ile Bölünebilme Kuralı
