Ardışık Tek Sayıların Toplamı
Bu yazıda ardışık tek sayıların toplamı nasıl bulunur bunu öğrenmeye çalışacağız. Hem ardışık tek sayıların toplamının formülü nedir bunu vereceğiz. Hem de formülün nasıl elde edildiğini öğreneceğiz. Böylece formülü hatırlamasak dahi bunu nasıl elde ettiğimizi bildiğimiz için her türlü soruyu çözebileceğiz.
Ardışık Sayılar
Art arda gelen sayılara ardışık sayılar denir. 1, 2, 3, 4, 5 şeklinde sıralanan sayılar ardışık sayıdır.
Ardışık tek sayılar sadece tek sayıların, ardışık çift sayılar ise sadece çift sayıların sıralanmasıdır.
- 1, 2, 3, 4, 5, 6 ... n şeklindeki sayılara ardışık sayılar denir.
- 2, 4, 6, , 10 ... 2n şeklindeki sayılara ardışık çift sayılar denir.
- 1, 3, 5, 7, 9 ... (2n - 1) şeklinde sıralanan sayılara ise ardışık tek sayılar denir.
Ardışık sayıların genel terimi n, ardışık çift sayıların genel terimi 2n, ardışık tek sayıların genel terimi ise (2n - 1) şeklindedir.
Daha önce ardışık çift doğal sayıların toplamının nasıl bulunacağını detaylıca öğrenmiştik: Ardışık çift sayıların toplamı
Ardışık Tek Sayıların Toplamı Nasıl Bulunur?
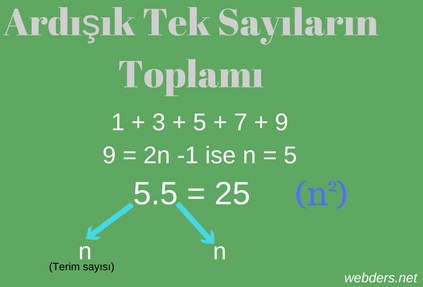
Bu konuda kullanabileceğimiz basit bir formül vardır. 1 + 3 + 5 + 7 + 9 + ... (2n - 1) = n2 formülü kullanılmaktadır. Bir örnekle formülü pekiştirelim.
Örnek: 1 + 3 + 5 + 7 ... + 19 toplamı kaçtır?
Çözüm: Dikkat edersek ardışık tek sayılar toplanmıştır. Burada genel terim (2n - 1) = 19 olur. Buradan da n = 10 bulunur. Öyleyse toplam n2 = 100 olacaktır.
Görüldüğü gibi basit bir formülle bu tür sorula çözebilmekteyiz.
Peki, 1'den başlamayan sorular için bu formülü nasıl kullanacağız?
Bu tür sorularda 1'den başlıyormuş gibi hesaplayıp aradaki farkı çıkararak cevabı kolaylıkla bulabiliriz.
Örneğin 9 + 11 + 13 ... 21 toplamını bulmak için 1'den 21'e kadar olan tek sayıların toplamını n2 formülüyle buluruz. Ardından 1'den 7'ye kadar olan sayıların toplamını bulduğumuz bu değerden çıkarırız. Böylece cevabı bulmuş oluruz.
Yani 1'den 21'e kadar olan sayıların toplamı 2n - 1 = 21 ⇒ n = 11 ⇒ n2 = 121 olur. Ardından 1'den 7'e kadar olan sayıların toplamı için 2n - 1 = 7 ⇒ n = 4 ⇒ n2 = 16 olur. 121 - 16'dan da cevabı 105 olarak buluruz.
Formülün İspatı
Yukarıda basitçe formülü nasıl kullanacağımızı öğrendik. Bu formül hem ilkokul hem lise hem de üniversite seviyesinde kullanılabilecek oldukça faydalı bir formüldür. Şimdi de formülün nereden geldiğini bulmaya çalışalım.
Ardışık sayıların toplamı (1 + 2 + 3 ... n şeklindeki toplam) n.(n + 1) / 2 formülü ile bulunmaktadır. Bunun nedeni terim sayısının yarısı kadar (n + 1)'in oluşmasıdır. Daha basit bir ifadeyle 1'den 100'e kadar sayıların toplamı 50.101 olacaktır. Çünkü 1 + 100 = 101, 2 + 99 = 101 ... 50 tane 101 elde edilecektir.
Eğer sadece çift sayıları toplarsak yani 2 + 4 + 6 şeklinde toplama yaparsak bunu 2 parantezine alarak yapabiliriz. Yani 2(1 + 2 + 3) şeklinde ifade edebiliriz. Bu durumda parantezin için yine ardışık sayılar olacaktır. Öyleyse 2.n.(n + 1) / 2 = n.(n + 1) olacaktır. Parantezi açarsak n2 + n sonucunu elde ederiz.
Ardışık tek sayılar da ardışık çift sayılardan 1'er çıkarılarak elde edilir. Yani 1 + 3 + 5 toplamı 2 + 4 + 6 toplamından 3 kadar eksiktir. Çünkü her terim için 1 eksik olmaktadır. Öyleyse aradaki fark terim sayısı kadar yani n kadar olmaktadır.
Ardışık tek sayıların formülünü elde etmek için de ardışık çift sayıların toplamından n çıkarmakla mümkündür. Öyleyse formül: (n2 + n) - n = n2 şeklinde elde edilecektir.
Ardışık Tek Sayılar ile İlgili Problemler
Tek sayıların toplamı formülü yukarıda detaylıca ispatı açıklanarak verilmiştir. Şimdi de konuyla ilgili problemler çözerek bilgimizi pekiştirelim.
Soru: 1’den 99’a kadar olan bütün tek sayıların toplamı kaçtır?
A) 2300
B) 2400
C) 2455
D) 2500
E) 2565
Çözüm: Yapmamız gereken ilk şey genel teriminin 2n - 1 olduğunu hatırlamaktır. Bütün tek sayıları 2n -1 şeklinde ifade edebiliriz. En büyük terim olan 99 için 2n - 1 = 99 olur. Buradan 2n = 100 ⇒ n = 50 olur. Tek sayıların toplamı ise n2 ⇒ 50.50 = 2500 bulunur. Cevap D seçeneğidir.
Soru: 41 + 43 + 45 + 47 ... 81 ardışık sayı dizisinin toplamı kaçtır?
A) 1691
B) 1587
C) 1387
D) 1293
E) 1281
Çözüm: Yukarıda bahsettiğimiz gibi 1'den başlayan diziler için n2 formülünü kullanmaktayız. Öyleyse önce 1'den 81'e kadar olan tek sayıların sayıların toplamını bulalım. Ardından da 1'den 39'a kadar olan tek sayıların toplamını bundan çıkarım.
1'den 81'e kadar olan sayıların toplamı 2n - 1 = 81 ⇒ n = 41, n2 = 41.41 = 1681 şeklinde bulunur.
Şimdi de 1'den 39'a kadar olan tek sayıların toplamını bulalım: 2n - 1 = 39 ⇒ n = 20, n2 = 20.20 = 400 olur.
Aradaki farkı almak için 1681 - 400 işlemini yaparsak cevap 1281 olur. Yani cevap E seçeneğidir.
Yukarıdaki iki örnek gibi çeşitli problemleri çözerek pratiğini arttırabilirsiniz. Eğer soru çözümlerini ya da formülü anlamadıysanız tekrar okumaya özen gösterin. Birkaç örnek soru çözdüğünüzde çok kolay olduğunu fark edeceksiniz.
Etiketler:
Son Eklenenler
- Tarımla İlgili Meslekler
- Matematiği İyi Olmayanlar Hangi Mesleği Seçmeli?
- Antropoloji Nedir?
- Dünyanın Kaç Türlü Hareketi Vardır?
- Toplumsal Düzeni Sağlayan Kurallar Nelerdir?
- Cumhuriyet Yönetiminin Değerleri Nelerdir?
- İklim ve Hava Olayları Arasındaki Fark
- 1 Asal Sayı Mıdır?
- Homeostasi nedir?
- 2 ile Bölünebilme Kuralı
