Asal Sayılar ve Özellikleri
Temel matematikte karşımıza çıkan en önemli konulardan biri asal sayılardır. Bu yazıda asal sayılar hakkında öğrenmemiz gereken her şeyi öğrenmeye çalışacağız.
İlk başta kolay ve gereksiz gelse de bize bilgisayarımız çalışmasına kadar birçok alanda asal sayıların yaygın olarak kullanıldığını bilmemiz gerekiyor. Matematikte ilerledikçe bu konunun karşımıza çok çıktığına da şahit olacaksınız.
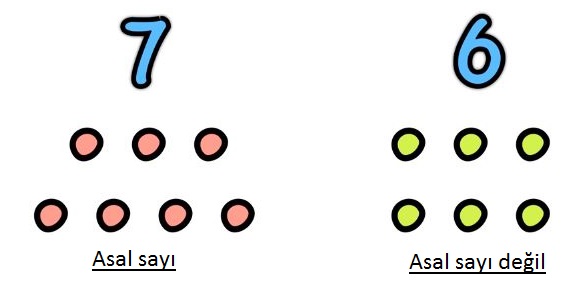
Asal sayılar 1’den büyük olmak zorundadır. Örneğin 7, 1 ve 7’e bölünür. Başka bir sayıya tam bölünmez. Bu nedenle 7 bir asal sayıdır. Ancak 6 sayısı 2, 3, 1 ve 6 sayılarına bölünür. Bu nedenle asal sayı değildir.
Asal Sayılar Konu Anlatımı
Asal sayılar matematikte temel kavramlardan itibaren karşımıza çıkan bir konudur. Örneğin matematikte bir asal çarpan olayı vardır. Asal çarpanlar bir sayıyı oluşturan çarpanlardır. Her sayı belirli sayıda asal sayıların çarpılmasıyla ortaya çıkar.
En küçük asal sayı 2’dir. 2 aynı zamanda asal sayı olan tek çift sayıdır.
Aşağıdaki asal sayılar tablosunda 200’e kadar asal sayılar gösterilmiştir.
| 2 | 3 | 5 | 7 | 11 | 13 | 17 | 19 |
| 23 | 29 | 31 | 37 | 41 | 43 | 47 | 53 |
| 59 | 61 | 67 | 71 | 73 | 79 | 83 | 89 |
| 97 | 101 | 103 | 107 | 109 | 113 | 127 | 131 |
| 137 | 139 | 149 | 151 | 157 | 163 | 167 | 173 |
| 179 | 181 | 191 | 193 | 197 | 199 |
Tablodan da anlaşılacağı gibi asal sayıların aralıkları sayılar büyüdükçe artmaktadır. Bir sayının asal olup olmadığını anlamak için önce onu en küçük asal sayı olan 2’ye böleriz. 2’ye tam bölünen bir sayı asal sayı değildir.
Eğer ikiye bölünmüyorsa sırasıyla 3’e 5’e ve devamına böleriz. Herhangi bir asal sayıya tam bölünüyorsa sayı asal sayı değildir.
Asal Çarpanlar
Yukarıda da belirttiğimiz gibi her sayı asal sayıların belirli oranda çarpılmasıyla ortaya çıkar.
Örneğin 30 sayısını ele alalım. 30’u çarpanlarına ayırdığımız zaman 2, 3 ve 5 ili çarpan olarak buluruz. Bu nedenle 30 = 21.31.51 asal çarpan açılımı elde edilir.
84 sayısını ele alalım. 84 = 22.71.31 olur. Asal çarpanların üstlerini 1’er arttırıp çarptığımız o sayının pozitif bölen sayısını elde ederiz. Yani 84’ün pozitif tam sayı bölen sayısı (2 + 1).(1 + 1). (1 + 1) = 12 olarak karşımıza çıkar. Bu yalnızca pozitif bölenleri içerir. 84’ün 12 tane de negatif tam böleni vardır. Yani 24 tane tam bölen elde edilebilir.
1 neden asal sayı değildir?
Bu soru asal sayılar konusunu çalışan herkesin karşısına çıkabilmektedir. Asal sayı aslında 2 farklı sayıya tam bölünmek zorundadır. 1 sadece 1’e tam bölündüğüne göre asal sayı değildir.
Asal Sayılar Soruları
Yukarıda öğrendiğimiz tanımlar üzerinden birkaç asal sayı soru örneği çözelim. Asal sayıların önemi sadece doğruda asal sayılar soruları ile ilgili değildir. Aynı zamanda başka konularda sorulan sorular içerisinde de asal sayı tanımı kullanılmaktadır.
Soru #1: Aşağıdaki sayılardan hangileri asal sayı değildir?
- 3
- 5
- 12
- 17
- 39
Çözüm: Sayılardan 12 çift sayı olduğu için 2’nin katıdır. Bu yüzden asal sayı değildir. 39 ise 3’ün katıdır bu yüzden asal değildir. Geriye kalan sayılar 3, 5 ve 17 sadece kendilerine ve 1’e tam bölünürler bu yüzden asal sayılardır.
Soru #2: Aşağıdaki sayılardan hangisi asal sayıdır?
- 6
- 21
- 37
- 51
- 91
Çözüm: Bu sayılardan 6, 21, 51 3'e bölünür. 91 ise 7'e bölünmektedir. Bu nedenle yalnızca 37 asal sayıdır.
Soru #3: 9a sayısı iki basamaklı bir sayıdır. Buna göre a sayısı hangi değerleri alabilir?
Çözüm: İki basamaklı asal sayılar çok sık karşımıza çıkar. 90 hem 2'ye hem 3'e hem de 5'e bölünebilmektedir. Öyleyse a sayısının bunların hiçbirinin katı olmaması gerekir. Aksi taktirde mutlaka bir asal sayıya bölünecektir. 0'dan 9'a kadar baktığımızda sadece 7 sayısının bu şartı sağladığını görüyoruz. Öyleyse a yalnızca 7 olabilir. Yukarıdaki tabloya baktığımız zaman 9 ile başlayan sadece 97 sayısının asal sayılar tablosunda yer aldığını görürüz.
Bununla ilgili bir örnek daha çözelim.
Soru #4: 5x sayısı iki basamaklı bir sayı olmak üzere x'in alabileceği değerler toplamı kaçtır?
Çözüm: Bir önceki örnekte kullandığımız yöntemi yeniden uygularsak sadece 53 ve 57 sayılarının bu şartı sağladığını görürüz. Öyleyse 3 ve 7 x'in alabileceği değerlerdir. Bu nedenle cevap 3 + 7 = 10 olur.
Asal sayıların tanımıyla ilgili de bir örnek çözelim.
Soru #5: Aşağıdaki sayılardan hangisi asal sayıdır?
A) -3
B) 13,5
C) 51
D) 73
E) 93
Çözüm: -3 negatif sayı olduğu için, 13,5 ise tam sayı olmadığı için asal sayı değildir. 51 ve 93 sayıları da 3'e tam bölünebilmektedir. Bu durumda cevap 73 yani D seçeneği olacaktır.
Etiketler:
Son Eklenenler
- Tarımla İlgili Meslekler
- Matematiği İyi Olmayanlar Hangi Mesleği Seçmeli?
- Antropoloji Nedir?
- Dünyanın Kaç Türlü Hareketi Vardır?
- Toplumsal Düzeni Sağlayan Kurallar Nelerdir?
- Cumhuriyet Yönetiminin Değerleri Nelerdir?
- İklim ve Hava Olayları Arasındaki Fark
- 1 Asal Sayı Mıdır?
- Homeostasi nedir?
- 2 ile Bölünebilme Kuralı
