Üçgende Benzerlik

Bir fotoğrafı ile onun büyütülmüş hali birbirine benzerdir. Bir yapının mini biblosu ona yine benzer özellik gösterir. Bir geometrik şeklin benzeri dediğimiz zaman onun belli bir oranda büyütülmüş ve küçültülmüş hali aklımıza gelir. Üçgenin boyutları değişse dahi kenar ve açıların oranı değişmeyeceği için oranlardan yola çıkarak işlem yapabiliriz. İşte üçgende benzerlik bunun üzerine kurulmuştur.

Bir eşkenar üçgeni büyütürsek açılar değişmez. Aynı oranda kenar uzunlukları büyür. Ancak yeni üçgen de eşkenar üçgen olmuş olur. Aynı şekilde sıradan bir üçgeni de alıp büyüttüğümüzde ya da küçülttüğümüzde elde ettiğimiz üçgenlere benzer üçgenler deriz.

İki üçgen arasında eşleşme yapıldığında açılar eşit, kenarlar orantılı ise bu üçgenler benzer üçgenlerdir. Zaten aynı üç açı derecesinden oluşan iki üçgen benzer olmak durumundadır.

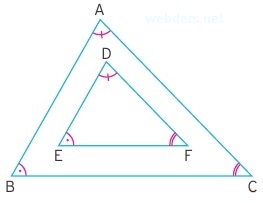
Yukarıdaki üçgende ABC üçgeni DEF üçgeninin benzer halidir. Fotokopi mantığıyla büyütülmüştür. Aynı açıların karşısındaki kenarlar birbiriyle orantılıdır. Mesela D açısı ile A açısı aynı olduğu için |BC| kenarı ile |EF| kenarları orantılıdır. Bu orantı diğer kenarlar için de aynen geçerlidir.

|AB| / |DE| = |AC| / |DF| = |BC| / |EF| = k eşitliği vardır. Burada k benzerlik oranı olarak karşımıza çıkar.

Üçgende Benzerlik Teoremleri

İki üçgenin açıları eşitse bu üçgenler benzer üçgenlerdir. İç içe üçgenlerde paralellik olduğunda yöndeşlikten dolayı açılar eşit olur. Bu durumda benzer üçgen elde edilmiş olur. Üçgende benzerlik teoremleri bu tarz üçgenlerde daha kolay uygulanır.

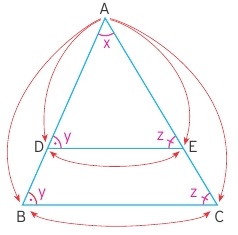
Yukarıdaki üçgende büyük ve küçük üçgenlerde açılar aynı olduğu için kenar uzunlukları orantılıdır. Üçgende benzerlik teoremleri içerisinde bu teorem hepsinin temelini oluşturur. O yüzden bu konunun öğrenilmesi için bu üçgen üzerindeki şekil iyi anlaşılmalıdır.

Üçgende |AD| / |AB| = |AE| / |AC| = |DE| / |BC| olur.

Bölme işleminde ortaya çıkan benzerlik oranı burada da vardır.

Üçgende benzerlik kuralları hep aynı mantıkla üretilmiştir. Aynı açının karşısındaki kenarların  arasında belirli bir orantı olmaktadır. Üçgende benzerlik soruları çözüldükçe konunun mantığı daha iyi kavranacaktır. Yukarıda öğrendiklerimizle ilgili bir örnek yapalım.

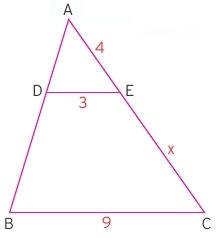
Yukarıdaki üçgende |DE| doğru parçası |BC| kenarına paralel olarak verilmiştir. Verilen kenar bilgilerine göre |EC| = x uzunluğunu bulunuz.

Çözüm: Paralelliğin olması yöndeş açıların eşit olması demektir. Tepe açısı olan A açısı da zaten iki üçgende ortak olduğu için benzer iki üçgen elde edilmiş olur. Benzer üçgenlerin aynı açıları karşısındaki kenarlar birbiriyle orantılıdır.

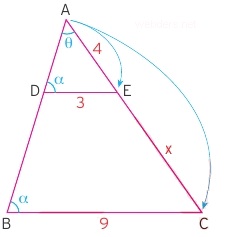
Buna göre 3 / 9 = 4 / (4 + x) olur. Buradan da 4 + x = 12 ⇒ x = 8 bulunur.

Üçgende benzerliği öğrenmek için üçgende benzerlik formüllerine ihtiyacınız yoktur. Sadece benzerliğin temel mantığını anlamanız yeterlidir. Yukarıdaki örneğin bir benzerini daha çözelim.

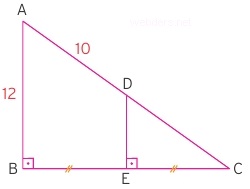
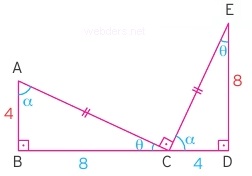
Yukarıdaki üçgende dik üçgen içerisinde başka bir dik üçgen verişmiştir. Buna göre küçük üçgen olan DEC üçgeninin çevresini bulunuz.

Çözüm: Soruda görüldüğü üzere iki tane diklik bulunmaktadır. Bize paralellik bilgisi verilmemiş olsa dahi aynı doğruya inen dikmelerin paralel olmak zorunda oldu biliyoruz.

Buna göre C açısı zaten ortak olduğu için D açısı A açısına, dik B açısı da dik E açısına eşit olmaktadır. Bu durumda küçük üçgen ile büyük üçgen benzerdir.

|EC| / |BC| = |DE| / |AB| = |DC| / |AC| oranları bulunmaktadır. Bu oranlardan herhangi birini bilirsek geri kalanına da doğrudan ulaşmış olacağız. Dikkat ederseniz soruda |BE| = |EC| eşitlik olarak verilmiştir. Öyleyse oranımız 1'e 2 oranı olmuş olur.

Bu durumda |DE| = 12/2 = 6 olur. |DC| = x dersek, x / (x + 10) = 1/2 olmak durumundadır. Buradan da x = 10 olmaktadır. Yani |AC| = 20 olmaktadır. Böylece büyük üçgende eksik sadece |BC| kenarı almaktadır. Pisagor bağıntısıyla 12,16,20 üçgeni çıkacağı için |BC| = 16, |EC| = 8 çıkacaktır.

Dikkat ederseniz 1'e 2 oranına göre büyük üçgen 12 - 16 - 20 üçgeni, küçük üçgen ise 6 - 8 - 10 üçgeni olmuştur. Küçük üçgenin çevresi de 6 + 8 + 10 = 24 olur.

Bu soruda hem benzerlik, hem Pisagor bağıntısı kullanılmıştır. 3 - 4 - 5 üçgeninin bütün katları zaten benzer olmak zorundadırlar. Bu üçgende açılar değişmemekte, sadece kenarlar belirli oranda büyümektedir. 3 ile orantılı kenarın karşısı 37 derece, 4 ile orantılı kenarın ölçüsü de 53 derece olmaktadır. Bunu da bilmeniz size dik üçgende pratiklik kazandıracaktır.

Üçgende Kelebek Benzerliği

Benzerlik teoremleri soru tiplerinden ibarettir. Karşımıza en çok çıkan soru tiplerinden biri de kelebek şeklinde çapraz duran çift üçgenli şekildir. Burada da paralellikten dolayı iki açı eşit olmakta, üçüncü açı ise çapraz açı olduğu için eşit çıkmaktadır. Üç açı eşit çıktığı zaman doğal olarak benzer üçgenler elde edilmiş olur. Kelebek benzerliğini şekil üzerinde gösterelim.

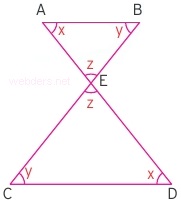
Yukarıdaki şekilde |AB| // |CD| paralelliği vardır. Bu paralellik bize eşit açılar vermektedir. Üç açı da eşit olduğunda yukarıdaki gibi iki üçgen benzer üçgen olurlar. Benzerlik oranı da eşit açılar arasında vardır. Kelebek benzerliğinde çapraz açılar eşit olduğunda benzerlik de çapraz kenarları arasında olur. Bir örnekle gösterelim.

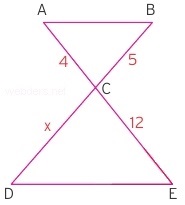
Yukarıdaki soruda x ile tanımlanmış kenar uzunluğu sorulmaktadır. Kelebek şeklinde aldanmak doğru olmaz. Soruda kelebek olması için paralelliğe ihtiyaç vardır. Bu soruda bu verilmiştir.

Buna göre 4 / 12 = 5 / x olur. Buradan da x = 15 çıkar.

Benzerlik konusunda çeşitli terimler vardır. Açı açı açı benzerliği, kenar açı kenar benzerliği gibi kavramlar karşımıza çıkabilir. Aslında bu kavramlarım çok manası yoktur. Benzerlik olması için üç açı da eşit olmalıdır. Açı açı açı benzerliği budur zaten. Kenar açı kenar benzerliği de bir açının eş olması ve kalan iki kenarın da orantılı olması sonucunda bize diğer açıların eşit olduğunu verir.

Üçgenlerin Eşliği

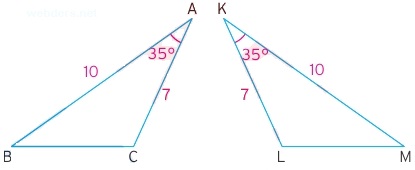
İki üçgen birebir aynıysa bu üçgenlere eş üçgenler denir. Eş güçler de benzerdir ancak benzerlik oranı k = 1 olur. Üç kenarı eşit olan iki üçgen mutlaka eş olur. Çünkü o kenar dağılımını sağlamak için aynı açıların olması gerekir. Kenar kenar kenar eşliği ile ilgili aşağıdaki örneğe bakınız.

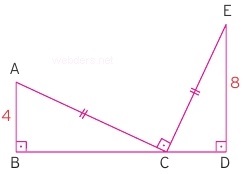
Örnekte iki üçgenin hipotenüs uzunluğu aynı verilmiştir. 90 derecelik bir açıları da aynıdır. Diğer açılara da harf verdiğimiz zaman açıların birbirini tümlediği ortaya çıkar.

Buna göre |BC| = |AD| = 8 olur. Aynı şekilde |AB| = |CD| = 4 olur. Bunun sebebi şudur. ECD açısına a dediğinizde ACB açısına da b dersiniz. Bu durumda a + b = 90 derece olduğu için karşı açılar da tümler olacaktır.

Kenar açı kenar eşliğinde ise iki kenar ve aradaki açı eşit olduğunda kosinüs teoremi gereği üçüncü kenar eşit olur. Üç kenar eşit olduğunda bu üçgenler de doğal olarak eş olmaktadır.

Yukarıdaki örnekte kenar açı kenar eşliğine örnek bir durum vardır. İki kenar ve aradaki açı eşit olduğu için bu üçgenlerin eş olduğunu doğrudan söyleyebiliriz. Burada asıl mesela eş kenarların arasındaki açının eşit olmasıdır.

Üçgende Benzerlik ve Alan

Üçgende benzerliğin alan ile doğrudan bir ilişkisi vardır. Benzerlik bir üçgenin belirli bir oranda büyütülmesi ve küçültülmesi ile elde edilmektedir. Doğal olarak büyüyen ve küçülen üçgenlerin alanları da değişecektir.

Sonuçta açılar aynı kalacağı için üçgenlerin benzer olduğunu söyleyebiliriz. Üçgende benzerlik oranı k'den bahsetmiştik. Benzerlik oranı k olan iki üçgenin alanları k² ile oranlıdır. Çünkü iki kenarın çarpılması sonucunda sinüslü alan formülü ile alan elde edildiği için k oranı çarpıma iki kez girecektir. Bu da k.k = k² eşitliğini ortaya çıkaracaktır.

Örneğin 6 - 8 - 10 üçgeni ile 3 - 4 - 5 üçgeni arasındaki benzerlik oranı k = 2 olur. Çünkü kenarlarının oranı 2'dir. Ancak alanları arasında k² = 4 oranı bulunur. Bir üçgen 6 br² iken diğeri 24 br² olur.