Eşkenar Dörtgen

Kenar uzunları aynı olan paralelkenara eşkenar dörtgen denir. Daha önce paralelkenar konusunda karşılıklı kenarların eşitliğinden bahsettik. Burada ise 4 kenarın hepsi eşit olmaktadır. Aslında kare de bir eşkenar dörtgendir ancak eşkenar dörtgende kenarların birbiriyle 90 derecelik açı yapması şartı aranmaz.

Süslü görüntüsünden dolay eşkenar dörtgen bazı modellerde kullanılmaktadır. Dört bir yanı eşit uzunlukta olan bir baklava dilimi eşkenar dörtgene güzel bir örnek olabilir.

Eşkenar Dörtgen Çizimi

Eşkenar dörtgeni cetvel ve pergel yardımıyla çizebiliriz. Şeklin nasıl çizildiğini bilirsek şekli tanımamız da o nispette kolay olacaktır. Eşkenar dörtgeni cetvel ve pergel kullanarak dört adımda çizebiliriz.

1. Adım: Cetvel yardımıyla |AB| doğru parçası çizeriz.

2. Adım: Pergeli |AB| uzunluğu kadar açıp A noktası merkezli bir yay çizeriz. Yay üzerinde uygun bir D noktası belirleriz.

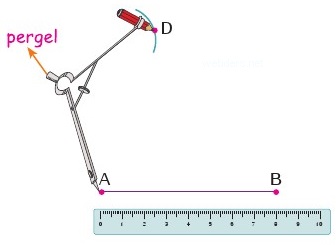
3. Adım: Pergelin açıklık miktarını bozmadan D ve B merkezli yaylar çizerek iki yayın kesiştiği C noktasını belirleriz.

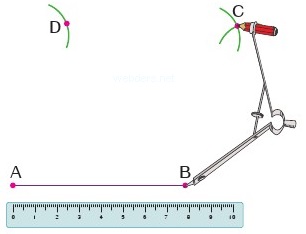
4. Adım: Elde edilen A, B, C, D noktalarını cetvel aracılığıyla birleştirerek eşkenar dörtgeni elde ederiz.

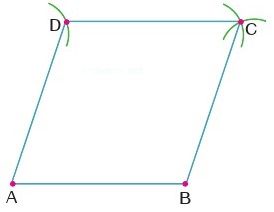
Çizdiğimiz şekilde 4 kenarın da uzunluğu ilk başta belirlediğimiz |AB| kenarı uzunluğunda olur. Böylece eşkenar dörtgen ortaya çıkmış olur.

Eşkenar Dörtgen Özellikleri

Eşkenar dörtgen aynı zamanda bir paralelkenar olduğu için paralelkenarın bütün özelliklerini aynen taşır. Bu nedenle farklı olan özellik dışındakiler verilmeyecektir. Dilerseniz paralelkenar konusuna tekrar göz atabilirsiniz.

Eşkenar dörtgen sıradan bir paralelkenara göre fazladan özellikle de gösterir. Bu özelliklerin sayısı çok değildir. Sadece eşkenar dörtgende köşegenler birbirini dik keser ve açıortay oluştururlar.

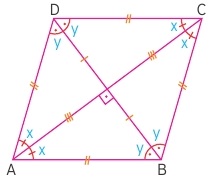
Yukarıdaki şekilde bir eşkenar dörtgen verilmiştir. Görüldüğü gibi köşegenler birbirini ortalamakta, dik kesişmekte ve açıortay özelliği göstermektedir. Ancak köşegen uzunlukları eşit değildir. Köşegenlerin uzunluğu eşit de çıkabilir fakat bu bir zorunluluk değildir. Buna dikkat etmek gerekir.

Eşkenar dörtgenin diğer bütün özellikleri için paralelkenar özelliklerine bakmak yeterli olacaktır. Eşkenar dörtgeni sadece paralelkenarın özel bir hali gibi düşünmekte fayda vardır.

Eşkenar Dörtgende Alanın Hesaplanması

Eşkenar dörtgende alan hesaplanırken kenarların herhangi biriyle o kenara ait yükseklik çarpılır. Bunun nedeni şudur. Kenarlar eşit olduğu için kenarlara ait yükseklikler de eşit olacaktır. Böylece hesaplama için basit ve genel bir formül ortaya çıkacaktır.

Yukarıdaki şekil eşkenar üçgende kenar uzunluğunu ve kenara ait yüksekliği göstermiştir. Bir kenarın uzunluğunu a, ona ait yükseklik uzunluğuna h dersek alan şöyle olur.

Alan = a.h formülüyle bulunur.

Bazı durumlarda kenar uzunluğu ve kenara ait yükseklik üzerinden gidemeyiz. Bu durumlarda ise köşegenleri kullanırız. Çünkü köşegenler birbirine diktir. Bir yerde diklik varsa orada alan vardır.

Birbirine zaten dik durumda olan köşegenlerin çarpımının yarısı yine bize alanı verir.

Şekikdeki eşkenar dörtgende alan şu formülle bulunur:

Alan = |AC|.|BD| / 2

Şimdi de alan ile ilgili örnek soru çözelim.

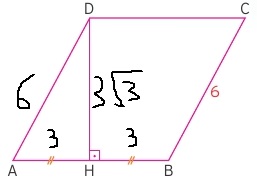
Örnek: Yukarıdaki eşkenar dörtgende bir kenar uzunluğu ile birlikte kenarı ikiye ayırmış yükseklik verilmiştir. Soruda bizden alanı bulmamız isteniyor.

Çözüm: Bütün kenarların uzunluğu eşit olduğuna göre |AB| kenarı da 6 birim olur. Bu durumda alanı hesaplamak için |DH| yüksekliğine ihtiyaç vardır.

|DH| yüksekliği özel üçgen bağıntısıyla çözülebilir. |AD| kenarı da 6 birim olduğundan 6 ve 3 oranıyla bu üçgenin bir 30 60 90 üçgeni olduğunu biliriz.

Buradan da |DH| yüksekliği 3√3 çıkacaktır. Alan ise 6.3√3 = 18√3 olacaktır.