Kare Konu Anlatımı

Çokgenler başlığında karşımıza çıkan geometrik şekillerden biri de karedir. Kare düzgün çokgen olması itibariyle görsel olarak güzel bir yapıya sahiptir.

Bu konu başlığı altında kare konu anlatımı ile birlikte örnekler yapılarak konunun kavranması sağlanacaktır.

Kare dört kenarlı düzgün çokgendir. Başka bir deyişle dört kenarının uzunluğu eşit olan diktörtgen karedir.

Kare aynı zamanda hem paralelkenar, eşkenar dörtgen hem de dikdörtgendir. Yani bahsedilen geometrik şekillerde geçerli olan bütün kurallar kare için de geçerlidir.

Karenin Çevresi ve Alanı

Bir kenarının uzunluğu x olan bir karenin çevresi 4x alanı ise x² şeklindedir. Aşağıdaki görselde bu durum gösterilmiştir.

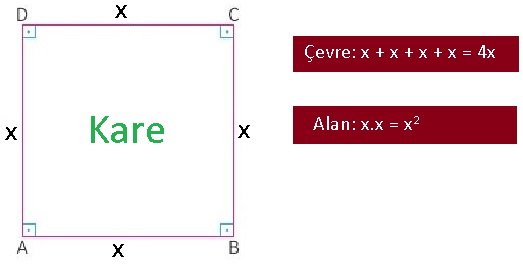
Karenin çevre ve alan hesabıyla ilgili çok basit bir örnek yapalım.

Örnek: Bir kenarı 3 cm olan bir karenin çevre ve alan büyüklüğünü hesaplayınız.

Çözüm: Karede çevre dört eşit kenarın uzunluğunun toplamı ile bulunur. Yani çevre 4.3 = 12 cm olur.

Karenin Özellikleri

Karenin özellikleri maddeler halinde şöyledir:

Dört kenarının da uzunluğu eşittir.
Çevresi 4a şeklindedir.
Alanı a2 şeklindedir.
Karşılıklı kenarlar paraleldir.
Komşu kenarlar diktir.
Köşegenler birbirini dik keser.
Köşegenler aynı zamanda açıortaydır.
Kare düzgün bir çokgendir.
Dört kenar da birbirini dik keser.
Köşegen uzunluğu kenar uzunluğunun √2 katıdır.

Yukarıdaki özellikler doğru kullanıldığında kare ile ilgili soruların büyük bir kısmı rahatlıkla çözülür.

Yukarıda da değinilen köşegen özelliklerini iyi bilmek gerekir. Kare sorularının çoğu köşegen özellikleri yardımıyla çözülür.

Aşağıdaki resimde kare köşegenlerin birbirini dik kestiği ve dört eşit parçalı bir yapının ortaya çıktığı gösterilmiştir.

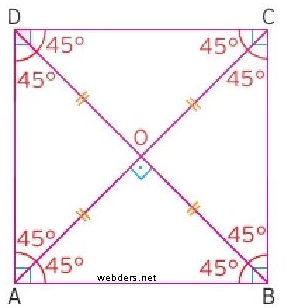
Aynı zamanda açıortay olan köşegenler iki adet 4 adet 45 - 45 - 90 üçgeni ortaya çıkarmıştır.

Kare Soruları

Kare konusu geometrideki diğer konular gibi çözüldükçe pekişen bir konudur. Bu nedenle konuyu öğrenmek için bolca soru çözmek gerekir. Zaten dikkat ederseniz kare için daha önce verilen özelliklerden farklı bir şey vermedik. Çünkü diğer çokgenlerde geçerli kurallar aynen karede de geçerlidir.

Örnek: Aşağıdaki karede DAE açısının ölçüsü EAB açısının ölçüsünün yarısıdır. Buna göre x açısının ölçüsünü bulunuz.

Çözüm: Şekilde görüldüğü gibi bir köşegen verilmiştir. Köşegenin dik açıyı iki adet 45 dereceye böldüğünü hemen göstermemiz gerekir.

Oranı verilen açıları da harflendirirsek sorunun çözümünde önemli adımlar atmış oluruz.

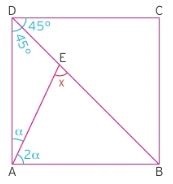
90 derecelik açıyı 3a şeklinde ifade edersek a ve 2a sırasıyla 30 ve 60 derece olur.

Üçgenin iç açılar toplamı 180 derece olduğuna göre şu bağıntıyı kurabiliriz. 60 + 45 + x = 180

Buradan da x = 75 derece çıkacaktır.

Bir de uzunluk ile ilgili bir soru çözelim.

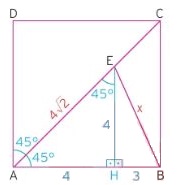
Örnek: Aşağıda verilen bilgiler ışığında x uzunluğunu bulunuz.

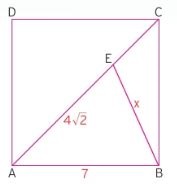
Çözüm: Köşegenin açıyı 45 derece olarak bölmesini kullanmak için E noktasından bir dikme indiririz. Bu dikmeyi indirdiğimiz anda soru kendiliğinden çıkacaktır zaten.