Çokgenler
Geometrinin birçok konusunu üçgenler üzerinde gördük. Aslında üçgenler birer çokgendirler. Kenarı sayısı 3 veya 3'ten büyük olan kapalı geometrik şekillere çokgen denir. Çokgenler içerisinde üçgenlerin ve dörtgenlerin özel konumu vardır. Bütün temel geometrik kavramlar buradan çıktığı için bunlar daha çok bilinir. Ancak bütün çokgenlerde ortak olan konular da çok önemlidir. Aşağıdaki şekilde birkaç basit çokgen örneği verilmiştir.
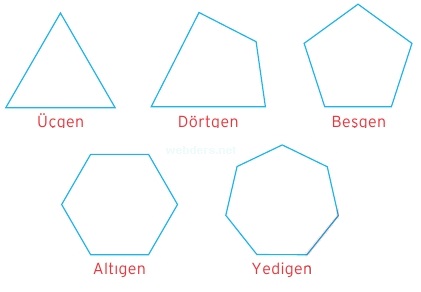
Bir çokgende köşeleri birleştiren doğru parçalarına çokgenin köşegenleri denir. Çokgenin etrafını oluşturan doğru parçaları ise çokgenin kenarlarıdır. Çokgeni isimlendirirken çokgenin kenar sayısı esas alınır. Mesela yedigen dediğimizde yedi kenarı olan bir çokgeni kast etmiş oluruz.
Bir çokgenin n tane kenarı olduğunu düşünelim. Kenar sayısı ile köşe sayısı eşit olduğu için n tane köşe demektir. Burada çokgenin her bir köşesinden kendisine ve en yakın iki komşusuna köşegen çizilemez. Bu nedenle n kenarlı bir çokgenin her bir köşesinden n - 3 tane köşegen çizilir. Bu durumda toplam köşegen sayısı n.(n - 3) olması beklenir. Ancak köşegenlerin tersten de çizilmesi söz konusu olduğu için 2'ye böleriz.
Bir çokgendeki köşegen sayısı: n.(n - 3)/2 olur.
Örnek olarak bir beşgeni düşünelim. Böyle bir çokgende kenar ve köşe sayısı n = 5 olur. Toplam köşegen sayısı ise 5.(5 - 3)/2 = 5 olur. Bir köşeden çizilebilecek köşegen ise 5 - 3 = 2 olur.
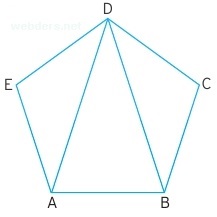
Bir çokgenin bir köşesinden n - 3 köşegen çizilir ve bu çokgeni n - 2 tane üçgensel bölgeye ayırır. Çokgenlerin de en alt birimi yine üçgenlerdir. Yukarıdaki beşgenin D köşesinde 2 köşegen çizilmiş ve beşgeni 3 üçgensel bölgeye ayırmıştır.
Soru: Köşegen sayısı kenar sayısının 2 katı olan çokgen kaç kenarlıdır?
Çözüm: n kenarlı bir çokgen düşülenelim. Köşeden sayısı n.(n-3)/2 olacaktır. Bu da kenar sayısının 2 katı olduğuna göre n.(n-3)/2 = 2n denklemi kurulur. Buradan da n = 7 çıkacaktır.
Çokgenlerde dış açı toplamı her zaman sabittir. Bu bilgi açı hesaplamalarında çok işimize yaramaktadır.
Soru: Bir yüzgenin dış açıları toplam derecesi kaçtır?
Cevap: 360 derecedir. Çünkü bütün çokgenlerin dış açıları toplamı 360 derecedir.
Düzgün Çokgenler
Bütün kenarlarının uzunlukları aynı olan çokgenlere düzgün çokgenler denir. Üçgenlerden bir tek eşkenar üçgen düzgün çokgen sınıfına girmektedir. Düzgün çokgenlerde kenar uzunlukları aynı olduğu için açı ölçüleri de aynıdır. Sabit bir iç açı ve sabit bir dış açı vardır. Dörtgenlerde ise düzgün dörtgen karedir.
Soru: Bir düzgün altıgenin bir iç açısı kaç derecedir.
Çözüm: Çokgenlerde iç açı hesaplamayı henüz görmedik. Ancak bütün çokgenlerin dış açıları toplamının 360 derece olduğunu öğrendik. Buna göre bir düzgün altıgenin de toplam dış açısı 360 olacağına göre bir dış açısı 360/6 = 60 derece olacaktır. Dış açı ile iç açı bütünler olduğu için bir iç açı da 120 derece olacaktır. Bu durumda altıgenin iç açıları toplamı da 6.120 = 720 derecedir. Eğer düzgünlük bozulursa açıların birbirinden farkı olabilir. Ancak 360 ve 720 toplam dereceleri değişmez.
Çokgende iç açılar toplam derecesi (n - 2).180 formülü ile bulunur. Bu hesaba göre çokgenlerde iç açılar toplamı;
- Üçgende 180
- Dörtgende 360
- Beşgende 540
- Altıgende 720
- Yedigende 800 derece olur.
Soru: Bir düzgün ongenin bir iç açısı kaç derecedir.
Çözüm: Çözüm için birden farklı yol kullanabiliriz.
I. Yol
Düzgün çokgende bütün iç açılar ve dış açılar birbirinin aynısı olduğu için bir dış açı 360 / 10 = 36 olur. Bütünler olan iç açı da 180 - 36 = 144 bulunur.
II. Yol
Bir çokgenin iç açıları toplam derecesi (n-2).180 formülüyle hesaplanmaktadır. Bu durumda bir ongenin iç açılar toplamı 8.180 = 1440 bulunur. Her bir açıya ise 1440 / 10 = 144 derece düşmüş olur.
Düzgün çokgenlerde her bir iç açının ölçüsü kenar sayısı arttıkça artar. Bir dış açının ölçüsü de toplam sabit olması itibariyle azalır.
| Düzgün çokgen | İç açılar toplamı | Dış açılar toplamı | İç açı | Dış açı |
|---|---|---|---|---|
| Üçgen | 180 | 360 | 60 | 120 |
| Dörtgen | 360 | 360 | 90 | 90 |
| Beşgen | 540 | 360 | 108 | 72 |
| Altıgen | 720 | 360 | 120 | 60 |
Yukarıdaki tablo düzgün çokgenlerden ilk dördünün açı durumlarını vermektedir. Bu değerler yukarıda verdiğimiz çokgen formülleriyle ortaya çıkmaktadır.
Düzgün Çokgenlerde Açı Hesaplamaları
Açı geometri için çok önemli bir kavramdır. Düzgün çokgenler de açıların hesaplanması açısından önemli mecralardır. Düzgün çokgenlerde pratiklik olması açısından dış açıların toplamının 360 derece olduğunu kullanmak çok mantıklıdır.
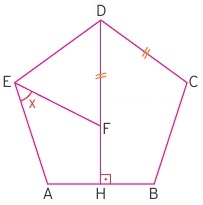
Yukarıdaki düzgün beşgende dikme indirilmiş ve x ile gösterilen açı sorulmaktadır.
Bu sorunun çözümü için üç tane temel işlemi yapmalıyız.
- Beşgenin kenarlarının eşitliğini kullanmalıyız.
- Beşgende her bir dış açısının 360/5 = 72 ve iç açının da 180 - 72 = 108 olduğunu bulmalıyız.
- Tepeden indirilen dikmenin açıyı ortalayacağını bilmeliyiz.
Eşitlikleri belirttiğimizde ve boş açıları yazdığımızda sonuç kendiliğinden çıkıyor zaten.
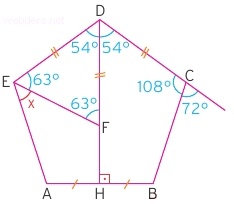
E açısı diğer iç açılar gibi 108 derece olacağı için x açısı 108 - 63 = 45 derece olur.
En Düzgün Çokgen Düzgün Altıgen
Düzgün altıgen içerisinde müthiş bir simetri barındırması itibariyle çok güzel bir çokgendir. Birçok özellik taşıyan bu özel çokgenin temel özelliklerini bilmemizde fayda vardır. Düzgün altıgende köşegenleri çizdiğimizde 6 tane eşkenar üçgen ortaya çıkar. İç açısı 120 derece, dış açısı 60 derece olması da bize birçok kolaylık sağlar.
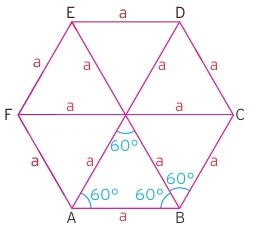
Normalde düzgün çokgenlerde alan hesaplaması yapılırken üçgensel bölgelere ayrılarak hesaplama yapılır. Ancak düzgün altıgenin 6 tane eşkenar üçgenden oluştuğunu biliyoruz. Bir eşkenar üçgenin alanının a2√3/4 olduğunu görmüştük. Öyleyse kenarı a olan yukarıdaki gibi düzgün bir altıgenin alının 6.a2√3/4 olduğunu söyleyebiliriz.
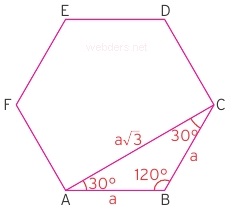
120 derecelik bir iç açının etrafındaki iki kenar da eşitse karşıdaki kenar √3 katı olur. Bu özellik de yine işimizi kolaylaştıran çokgen özellikleri arasındadır. Yukarıdaki şekilde bir iç açı 90 derece olduğu için ACD açısı 90 derecedir diyebiliriz. Çünkü iç açıyı tamamlayan 30 derecelik bir açı dışarıda kalmıştır. Yani |AC|, |DC|'ye diktir diyebiliriz.
Çokgenlerde Konveks ve Konkav Durumu
Çokgenler konusunda ve özel dörtgenlerin hepsinde genellikle konveks şekillerle işlem yaparız. Aslında bir şeklin çokgenler sınıfına girmesi için konvekslik şart değildir. Konkav şekiller de üçten fazla kenar sayısına sahip oldukları sürece çokgen sayılırlar. Ancak konkav (iç bükey) şekillerde farklı kurallar geçerli olmaktadır. Bizim daha çok ilgi alanımızda konvenks (dış bükey) geometrik şekiller bulunmaktadır.
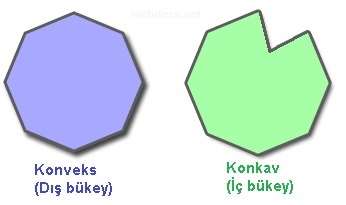
Yukarıdaki şekilde iki tane sekizgen bulunmaktadır. Bunlardan biri konveks iken diğeri konkav yani iç bükeydir. Aradaki farkı bu şekilde anlayabilirsiniz.
