Trigonometri Konu Anlatımı

Matematikte öğrencilerin en çok zorlandığı konuların başında trigonometri gelir. Bu ders notunda trigonometriyi basitleştirerek anlatacağız. Konuyu biraz öğrendikçe zor olmadığını, aksine zevkli olduğunu fark edeceksiniz. Trigonometriyi öğrenmek özellikle türev ve integral konularında çok işimize yarayacaktır. Bu nedenle konuyu dikkatlice detaylı çalışmanızı tavsiye ediyoruz.

Bir açıyı çizmek için iki kenara ihtiyacımız vardır. Açıyı daraltıp genişlettikçe bu iki kenarın birbirine göre durumları da değişecektir. Bu nedenle her açının kendine ait bir uzunluk oranı vardır. Bu oranı en iyi dik üçgende görebiliriz.

Matematiğin açı ve kenar arasındaki ilişkileri inceleyen dalına trigonometri deriz.

Temel Trigonometrik İfadeler

En temel dört tane trigonometrik ifade vardır:

• Sinüs (sin)
• Kosinüs (cos)
• Tanjant (tan)
• Kotanjant (cot)

Bunları dik üçgen üzerinde gösterelim. Böylece temel trigonometrik ifadelerin dik üçgen üzerinden nasıl ortaya çıktığını anlarız.

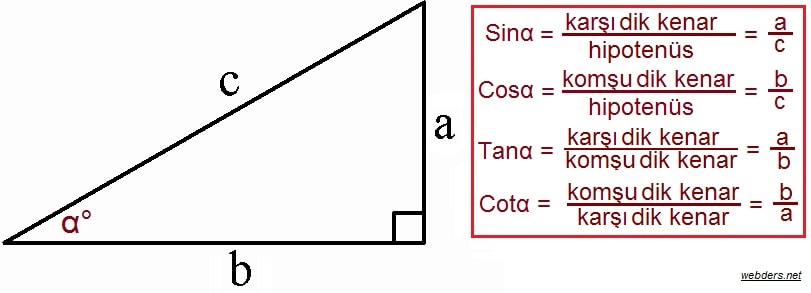
Yukarıdaki üçgende verilen eşitliklerin çok iyi anlaşılması gerekir. Bu eşitlikler anlaşılırsa konunun geri kalanı daha iyi anlaşılacaktır.

Öyleyse yukarıda denklemlerden tanα = sinα / cosα ve cotα = cosα / sinα bulunacaktır. Bunları kendiniz de deneyip ispatlayabilirsiniz. Hatta bunu yapmanız çok da iyi olacaktır. Buradan tanα = 1/cotα ve cotα = 1/tanα bulunacaktır. Yani tanjant ve kotanjant birbirinin tersi fonksiyonlardır. Dolayısıyla tanα.cotα = 1 olacaktır.

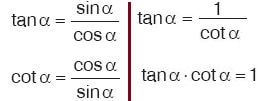
Tanjant ve kotanjant arasındaki ilişkiyi iyi bilmek çok önemlidir.

Soru: tan32°.cot32° = ? Çözüm: Açı aynı olduğu zaman tan.cot çarpımı 1'e eşit olur.

Tümler İki Açı Arasındaki Trogonometrik Eşitlikler

Toplamları 90° olan açılara tümler açılar denir. Örneğin 50° ile 40° tümler iki açıdır. Temel trigonometrik ifadeleri dik üçgen üzerinden tanımlamıştık. Öyleyse bir açının sinüsü diğer açının kosinüsü olacaktır. Buradan da şu eşitlikler çıkacaktır:

• Sekant (sec) = 1/cos
• Kosekant (cosec) = 1/sin

Tümler açılarla ilgili eşitlikleri trigonometrinin her seviyesinde kullanmaktayız. Bu nedenle bu konuyla ilgili bol miktarda soru çözmek gerekir.

Soru: sin42° / cos48° + cos48° / sin42° işleminin sonucu kaçtır?

Çözüm: 42 ve 48 tümler açılardır. yani toplamları 90 etmektedir. Öyleyse bu açılardan birinin sinüsü diğerinin kosinüsüne eşittir. Bu nedenle cevap 1 + 1 = 2 olacaktır.

Sinüs ve kosinüs arasında aynı açı için sin²x + cos²x = 1 eşitliği vardır. Bu eşitlik çok ama çok önemlidir.

Yarım Açı Formülleri

Yarım açı formülleri trigonometri ile ilgili soruların en çok sorulduğu alanlardan biridir. Sinüs ve Kosinüs ile ilgili yarım açı formüllerini bilmek sizin için yeterli olacaktır. Ancak dilerseniz Tanjant ve Kotanjant için de yarım açı formüllerini öğrenebilirsiniz.

• Sin2x = 2.sinx.cosx
• Cos2x = cos²x - sin²x = 2cos²x - 1 = 1 - 2sin²x
• Tan2x = 2tanx / (1 - tan²x)
• Cot2x = (Cot²x - 1) / 2cotx

Dikkat ederseniz cos2x için üç tane eşitlik paylaştık. Ana eşitlik Cos2x = cos²x - sin²x şeklindedir. Ancak sin²x + cos²x = 1 eşitliğini de işin içine kattığımızda diğer formüller de ortaya çıkmaktadır.

Birim Çember

Birim çember trigonometrinin genel mantığını anlamamıza yarayan mükemmel bir yöntemdir. Birim çember denmesinin sebebi koordinat düzleminde yarıçapı 1 birim olan bir çember olarak kabul edilmesidir.

Trigonometriye göre bir tam çemberin gösterdiği açı 360° ve 2π radyandır. İster derece cinsinden ister radyan cinsinden gösterilsin bu iki durum arasında fark yoktur.

Birim çemberi öğrenmek hem trigonometrik dönüşümleri öğrenmek hem de hangi aralıklarda sinüs, kosinüs, tanjant ve kotanjantın pozitif veya negatif olduğunu anlamak için çok önemlidir. Bu nedenle birim çemberi iyi analiz etmeliyiz.