Kütle Çekimi ve Kepler Kanunları

Gezegenlerin Hareketi

Dünya’nın kendi etrafında dönme ekseni Güneş etra­fında dönerken oluşan düzleme dik çizgi ile 23,5° lik bir açı yapar. Mevsimlerin oluşmasında bu eğiklik rol oynar. Dünya’mızın dönme ekseni, bir yalpalama ha­reketi yapar. Bu harekelin nedeni Güneş ve Ay'ın Dünya’ya etki ettirdikleri kütle çekim kuvvetlerinin küçük bir tork oluşturmasıdır. Ancak Dünyamızın bu yalpala­ma hareketinin periyodu 26.000 yıl olduğu için bunu gözlemlemek çok zordur.

Kutup yıldızının sürekli kuzeyde olmasının nedeni, Dünyanın kendi etrafında dönme ekseninin uzantısının Kutup yıldızından geçiyor olmasıdır. Ancak örneğin 5000 yıl önce kutup yıldızımız Alfa Draconis adlı başka bir yıldızdı. 5000 yıl sonra ise Dünya’nın yalpalama hareketinin sonucu olarak kutup yıldızımız Alfa Sephei adlı yıldız olacaktır.

Bir ipin ucuna bağlı m kütleli cisim r yarıçaplı yörüngede sabit açı­sal hızla döndürülür­ken sabit bir açısal momentuma sahiptir.

Ancak cismin bağlı ol­duğu ip çekilerek dön­me yarıçapı azaltıldı­ğında cismin açısal hızının arttığı gözlenir. Bu durum cismin açısal momentumunun korunumunun bir so­nucudur. Benzer bir durum gezegenlerin yıldızları etra­fındaki hareketleri için de geçerlidir.

Kepler Yasaları

Güneş sistemindeki gezegenlerin yörüngeleri üzerin­deki hareketlerinin özellikleri Kepler kanunları olarak bilinen üç kanun ile incelenir.

1. Yörüngeler Kanunu

Her gezegen, odak­larından birinde Gü­neş’in bulunduğu elips yörüngede ha­reket eder.

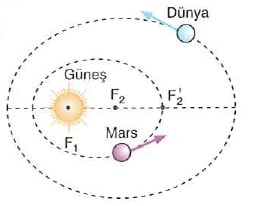
Şekilde 1. kanuna göre, Dünya ve Mars’ın elips yörüngeleri çizilmiştir. Dünya’nın elips yörüngesinin odak noktaları F₁ ve F’₂ dir. Mars’ın yörüngesinin odak noktaları F₁ ve F₂ dir. Güneş bu ge­zegenlerin yörüngelerinin ortak odak noktasında bulu­nur. F₁ noktası diğer gezegenlerin elips yörüngelerinin ortak odak noktasıdır.

2. Alanlar Kanunu

Gezegeni Güneş’e birleştiren yarıçap vektörü, eşit zaman­larda eşit alanlar tarar.

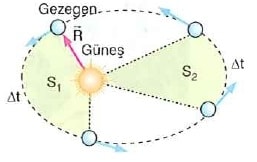
Şekilde, Δt sürede taranan S₁ alanı, yi­ne Δt sürede taranan S₂ alanına eşittir. Bu süreler için­de gezegenin aldığı yol eşit olmadığından hızı da eşit olamaz. Bunun sonucu olarak gezegen Güneş’e yak­laştıkça hızı artar, uzaklaştıkça da hızı azalır.

Bu durum da Dünya'mızın açısal momentumunun ko­runuyor olmasının bir sonucudur.

3. Periyotlar Kanunu

Gezegenlerin yörüngelerinin ortalama yarıçapları R ve periyotları (bir turları için geçen süre ) T olmak üzere, R³/T² oranı bütün gezegenler için aynıdır. Bu değer 3,4.10⁸'e eşittir. 

Gezegenlerin yörün­gelerinin ortalama yarı­çapları, Güneşe olan maksimum ve minimum uzaklıklar toplamının yarısıdır. Ortalama yarıçap;

R_ort = (R_max + R_min)/2 şeklinde bulunur.

Kütle Çekimi

Bilinen temel kuvvetlerden dördüncüsü olan kütle çe­kim kuvveti en zayıf kuvvet olmakla birlikte etki alanı en büyük olan kuvvettir.

Moleküllerden, gezegenlere, gezegenlerden evrenin en uç noktalarına kadar etkileri görülmektedir.

Dünya, kütlesinden dolayı çevre­sindeki bütün cisimleri kendi mer­kezine doğru çeken bir kuvvetin kaynağıdır. Bu kuvvete yer çekim kuvveti denir. Yer çekimi kuvveti Dünya üzerindeki kütlesi ister bü­yük ister küçük olsun her varlığa uygulanır.

Buna göre, aralarında belli bir uzaklık bulunan iki ci­sim birbirlerine çekim kuvveti uygular. Yapılan deney ve gözlemlere göre çekim kuvveti, kütlelerin çarpımı ile doğru, aralarındaki uzaklığın karesi ile ters orantılı­dır.

F = α.m₁.m₂/R²

Bu orantıyı eşitlik ha­line getirebilmek için, ifade G gibi sabit sayı ile çarpılmalıdır.

Çekim kuvveti,

F = G.m₁.m₂/R² bağıntısı ile hesaplanır. 

Newton'un bulduğu bu kanuna genel çekim kanunu denir. Burada G sabit değeri,

6,67.10^-11 olarak bulunur.

Bu G sabitine evrensel çekim sabiti denir ve uzayın her yeri için aynı sayısal değer geçerlidir. 

Çekim İvmesi

Kütlesi sabit olan gezegenin yü­zeyindeki bir cisme uyguladığı çekim kuvveti, çekim kanununa göre bu cismin kütlesi ile orantı­lıdır. Cisme uygulanan çekim kuvveti cismin ağırlık kuvvetine eşittir. Çekim ivmesi,

F = G.M.m/R² bağıntısından m.g = G.M.m/R² eşitliğini kullanırsak g = G.M/R² bağıntısı elde edilir.

Gezegenin yüzeyinde­ki çekim ivmesi maksi­mumdur. Yüzeyden uzaklaştıkça çekim iv­mesi azalır. Örneğin yer yüzeyinden yer ya­rıçapı kadar yüksekteki çekim ivmesi,

g' = G.M/(R + R)² dir. Yer yüzeyindeki bağıntıyla kıyasladığımızda g' = G.M/4.R² = g/4 olur. 

Yani, yer yüzeyinden R kadar yüksekteki çekim iv­mesi, yer yüzeyindekinin dörtte biri kadardır.

Yerin merkezine doğru gidildikçe çekim ivmesi yer yarıçapı ile doğru orantılı olarak azalır ve merkez­de sıfır olur. Buna göre, yer merkezinden uzaklaş­tıkça çekim ivmesinin nasıl değiştiği şekildeki grafikle de ifade edilmiştir.

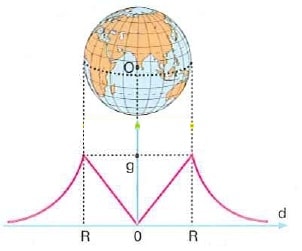
Dünya kutuplardan basık olduğu için yer merkezi­nin ekvatora olan uzaklığı kutuplara olan uzaklığın­dan daha fazladır. Dolayısıyla bir cismin kutuplar­daki ağırlığı, ekvatordaki ağırlığından daha fazla­dır. Ekvatordan kutuplara doğru gidildikçe cismin ağırlığı artar.

Bu artışta yarıçap değişiminin yanı sıra merkezkaç kuvvetinin değişimi de etkilidir. Merkezkaç kuvveti ekvatorda maksimum, kutuplarda ise sıfırdır. Mer­kezkaç kuvvetinin büyük olması ağırlık etkisinin daha az olmasına neden olmaktadır.

Kütlelerin büyük­lüğü ne olursa ol­sun karşılıklı çe­kim kuvvetleri eşit büyüklükte ve zıt yönlüdür. Bütün kütlenin, kütle merkezinde toplandığı varsayılacaktır.

F = -F₂

Dünyanın küçük bir cisme uyguladığı çekim kuvve­ti ile cismin dünyaya uyguladığı çekim kuvveti eşit midir? Evet eşittir. Ama niçin cisim dünyanın üzeri­ne düşüyor? diye sorulursa; dinamiğin temel pren­sibi F = m.a ya göre kuvvetler eşit olsalar bile dün­yanın kütlesi cismin kütlesine kıyaslanamayacak derecede büyük olduğundan cismin çekim kuvveti dünyaya hareket veremez. Dünya cisme hareket verir ve onu kendine doğru hızlandırır.

Kütle Çekim Potansiyel Enerjisi

Yer çekimi kuvvetinin sonucu olarak yer çe­kimi potansiyel enerjisi ortaya çıkmıştır. Ben­zer şekilde, genel kütle çekim kuvvetinin sonu­cu olarak da genel çe­kim potansiyel enerjisi tanımlanmaktadır.

M kütleli yer küre çevresinde r, yarıçaplı yörüngede do­lanan m kütleli uydunun kinetik enerjisinin yanı sıra bir­de kütle çekim potansiyel enerjisi vardır.

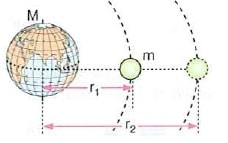
Bir cismi r₁ uzak­lığından r₂ uzaklı­ğına götürmek için çekim kuvve­tine karşı iş yapıl­ması gerekir. Bu iş kuvvet - uzaklık grafiğindeki taralı alana eşittir. 

Taralı alan = G.M.m(1/r₁ - 1/r₂) bağıntısıyla bulunur.

Buna göre, M kütleli bir gezegenden r kadar uzaklıkta­ki bir m kütleli cismin sahip olduğu çekim potansiyel enerjisi,

E_p = -GMm/r bağıntısıyla bulunur.

Bu bağıntıya göre, cisim gezegenden uzaklaştıkça çe­kim potansiyel enerjisi artar. Çünkü (-) li bir terimin kü­çülmesi büyümesi anlamına gelir.

Gezegenler Güneş etrafında elips yörüngelerde dola­nırken, Güneş’ten uzaklaştıkça kütle çekim potansiyel enerjisi artar, kinetik enerjisi ise azalır, ikisinin toplamı sabittir.

E_top = E_k + E_p

M kütleli gezegen etrafında dolanan m kütleli uydudan oluşmuş sistemin toplam mekanik enerjisi,

E_T = 1/2.m.v² - G.M.m/r şeklinde ifade edilir.

Yörünge boyunca uydunun toplam enerjisi daima sa­bittir. Gezegen Güneş’ten uzaklaştıkça potansiyel ener­ji artar, kinetik enerji azalır.

Kurtulma Enerjisi

Bir roketin Dünya’nın çekim alanından kurtulması için rokete çekim potansiyel enerjisi kadar kinetik enerji verilmelidir.

Bir cismi yerin çekim alanından kurtarmak, onu sonsu­za götürmekle sağlanır. Sonsuz uzaklıkta cismin top­lam potansiyel enerjisinin sıfır olması için ona verilme­si gereken minimum kinetik enerji,

Ek = G.M.m/r olur.

Bu enerji m kütleli bir cismi yerin çekim alanından kur­taracak en küçük enerjidir. Bu enerji cismin kurtulma enerjisine eşittir. Buradan bulunan hıza da kurtulma hızı denir.

E_k = 1/2.m.v² = G.M.m/r eşitliğinden v_kur = 2.√(G.M/r) olur.

Bağlanma Enerjisi

Yeryüzündeki bir cisim gibi, yür kürenin çevresinde dolanmakta olan bir uydu da yerin çekim alanı içindedir. Bu sebeple yere bir enerji ile bağlıdır. 

Bir uydu R yarıçaplı bir yörüngede dolanmakta ise ona etkiyen merkezcil kuvvet yerin uyguladığı çekim kuv­veti tarafından sağlanır.

1/2m.v² = G.M.m/2R olur.

Bu bağıntıya göre uydunun Dünya etrafında dolanabil­mesi için gerekli olan kinetik enerji, bulunduğu yerde­ki çekim potansiyel enerjisinin yarısına eşittir. Yani bir uyduyu Dünya çevresinde bir yörüngeye oturtmak için ona verilmesi gereken enerji ona Dünya’nın çekim ala­nından kurtarmak için gerekli enerjinin yarısına eşittir. Bu enerjiye uydunun bağlanma enerjisi denir.

E_b = G.M.m/2R şeklindedir.

Bir cismin toplam enerjisi negatif olduğu zaman cisim sisteme bağlanma enerjisi kadar bir enerjiyle bağlıdır.

Bağlanma enerjisi toplam enerjinin zıt işaretlisine eşit­tir. E_b = -E_t dir.