Bağıl Hareket

Belli bir hızla giden araçtan baktığımız­da yol kenarında duran kaldırım taş­larını, durakta oto­büs bekleyen insan­ları geriye doğru gi­diyormuş gibi görürüz. Yani hareketli araçlar üzerinde iken başka varlıkla­ra baktığımızda onları gerçek hızlarında yani yere gö­re hızlarında göremeyiz.

Cisimlerin birbirine göre hareketlerinin farklı algılan­masının nedeni hızlarının ya da hareket yönlerinin farklı oluşundandır.

Bir cismin, duran ya da hareket eden başka bir cisme göre yaptığı harekete bağıl hareket denir. Cisimlerin hızı ve hareket yönü gözlemcinin hızı ve hareket yönü­ne göre ya da seçilen başlangıç noktasına göre deği­şebilir.

Bağıl hız: Bir cismin hızının duran ya da hareket eden başka bir cisme göre hızıdır. v_b ile gösterilir. Vektörel bir niceliktir. Birimi m/s dir.

Bağıl hareket sorularında genellikle gözlenen ve gözlemcinin hangisinden hangisine bakmak gerektiği karıştırılır. Unutmayalım ki bağıl hızı bulmak için gözlenenden gözlemciyi çıkarmalıyız. 

v_bağıl = v_gözlenen - v_gözlemci

bağıntısı ile hesaplanır.

Bağıl hız vektörel olduğu için, işlemler vektörlerin özel­liklerine göre yapılır.

Bağıntıya göre, bağıl hız bulunurken, gözlediğimiz cis­min hızı aynen alınıp, gözlemcinin hızı ters çevrilerek vektörel olarak toplanır. Bu toplam vektör bağıl hızı ve­rir. Ya da bağıl hız bulunurken, gözlenen cisim hız vek­törü ile gözlemcinin hız vektörü çakıştırılır. Gözlemci­nin hız vektörünün ucundan, gözlenenin hız vektörü­nün ucuna çizilen vektör bağıl hızı verir.

Araçlar aynı doğrultuda hareket ediyorlarsa;

1. Aynı yönde gittiklerinde birbirlerine göre bağıl hız, hızlarının farkına eşittir.
2. Zıt yönlü gidi­yorlarsa, bir­birlerine göre bağıl hız, hızlarının toplamına eşittir.

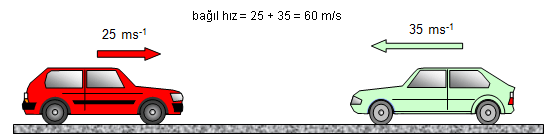
İki Boyutta Bağıl Hareket

Doğuya doğru gitmekte olan K aracının sürücüsü, ku­zeye doğru giden L aracının gerçek hareket yönünü ve hızını göremez. L nin K yi gördüğü hız bağıl hızdır.

Örneğin her iki araç v hızı ile gidiyorsa, K nin L ye göre hızı denildi­ğinde, L gözlemci olur. Gözlenen K cisminin hızı aynen alınır, göz­lemcinin hızı ters çevrilerek vektö­rel olarak toplanır. Hızların şiddet­leri eşit ve aralarındaki açı 90° olduğundan bağıl hız v√2 çıkar. Yani L'nin K'ye göre hızı;

v_b = v_L - v_K şeklinde bulunur.

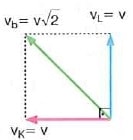
L nin hızı aynen alınır, K nin hızı ters çevrilerek toplanır. Hız vektörleri arasındaki açı 90° olduğundan bağıl hız v√2 olur. Yani araçların birbirleri­ne göre bağıl hızları eşit büyüklükte fakat zıt yönlüdür.

Irmak Problemleri

Irmak problemleri (nehir problemleri) ırmakta hareket eden kayıkların hız problemleri şeklindedir. Tek boyutta ve iki boyutta ırmak problemleri olarak ikiye ayrılır. 

Tek boyutta ırmak problemleri

Yalnızca yatay yönde yüzücü ve kayıkların hareket ettiği ırmak problemleridir. Yukarıdaki hız bağıntısı aynen kullanılır. Akıntıyla aynı yönde hareket eden cisimlere akıntının hızı eklenir. Akıntıya karşı hareket eden cisimlerin hızlarından akıntı hızı çıkarılır. Akıntı eklenip çıkarıldıktan sonra elde edilen hıza yere göre hız denir.

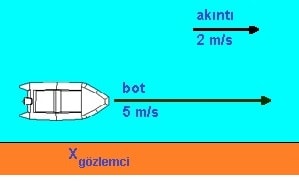
Yukarıdaki sistemde yerde hareketsiz duran X gözlemcisi botu 7 m/s hızla gidiyor şekilde görür. Çünkü akıntı 2 m/s hızla aynı yönde akmakta ve bota ilerlemede yardımcı olmaktadır. Botun suya göre hızı 5 m/s iken yere göre hızı 5 + 2 = 7 m/s şeklindedir. 

Bu hesaplamalar yapılırken akıntı hızının nehrin her yerinde aynı olduğu ve hareket eden cismin de sabit hızla hareket ettiği varsayılır.

Eğer akıntı ile yüzücü zıt yönde hareket ediyorsa yere göre hız bulunurken hızların farkı alınır.

İki boyutta ırmak problemleri

Irmağa göre düşey yönde de hareketlerin olduğu ırmak problemleridir. Bileşke hız vektörel toplam kurallarına göre bulunur.

Suya dik giren bir yüzücü akıntının etkisiyle yatay yönde saparak karşıya geçer. 

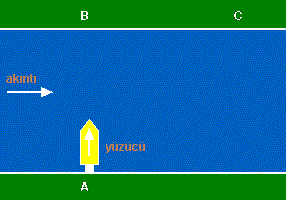
Şekilde A noktasından dik olarak suya giren yüzücü B noktasından karşıya çıkmayı hedeflerken C noktasından çıkmaktadır. Şimdi bu örneği sayısal verilerle tekrar inceleyelim. 

|AB| = 30 metre, |BC| = 40 metre olsun. Yüzücünün suya göre hızı da düşey yönde 3 m/s olsun. 

Bu durumda yüzücünün karşıya geçme süresi yalnızca nehrin genişliği (|AB| mesafesi) ve yüzücünün düşey hızıyla alakalıdır. 30/3 = 10 saniyedir. 

Karşıya geçme süresi 10 saniye olduğuna göre yüzücü su içerisinde 10 saniye geçirecektir demektir. Bu süre içerisinde yüzücünün sapmasına yalnızca akıntı etki etmektedir. 10 saniyede akıntıyla |BC| mesafesi kadar yani 40 metre sapması için akıntı hızının 40/10 = 4 m/s olmalıdır. 

Son olarak yüzücünün yere göre hızını bulalım. 

Yüzücünün yere göre hızı suya göre hızı ile akıntı hızının bileşkesi şeklindedir. Düşey yönde 3 m/s ile yatay yönde 4 m/s hızın bileşkesi vektörel toplam kurallarıyla bulunur. 

Birbirine dik olarak iki vektörün bileşkesi bulunurken Pisagor bağıntısı kullanılır. Yani 3² + 4² = R² buradan R = 5 m/s olarak bulunur.