Düzlem Geometride Temel Elemanlar ve İspat Biçimleri

Düzlem geometri birçok kabule dayanır. Geometri öğrenmek için düzlem geometride temel elemanları ve ispat biçimlerini bilmemiz gerekir. Bunu bilirsek daha sonraki konuların nereye dayandığını da önceden anlamış oluruz.

Aşağıdaki diyalog düzlem geometriye giriş için iyi bir problem içeriyor.

Ahmet ile ispat yapmayı seven Cemal arasında şöyle bir diyalog geçiyor:

Ahmet: Sevgili Cemal, üçgenin iç açılarının ölçüleri toplamı kaç derecedir?

Cemal: Bundan kolay ne var ki, elbette 180° dir.

Ahmet: Peki bunu ispatlayabilir misin?

Cemal: Tabi ki; bak şimdi A köşesinden [BC] ke­narına paralel olacak şekilde bir doğru çiziyorum ... ve şu iç ters açılardan . . . gördüğün gibi iç açıların toplamı 180° çıkıyor.

Dur bakalım Cemal, peki A köşesinden [BC] ye paralel olacak şekilde başka bir para­lel doğru çizilemez mi?

Ali bu soruya doğru cevap verecekse geometri­deki temel kabulleri (aksiyom ya da postulatları) iyi bilmelidir.

Postulat (Aksiyom)

Geometride doğruluğu açık olan ve ispata gerek duyulmadan kabul edilen önermelere "postulat" denir.

Postulat belirlemede temel amaç başlangıç noktasını belirlemek ve onun üzerine temel kurabil­mektir.

Postulatlar, teoremlerin ispatlarında ya da geo­metrik problemlerin çözümünde kullanılır.

Temel Beş Postulat

Geometrinin temelini oluşturan Öklid'in beş postulatı vardır. Bunlar temel aksiyomlardır. Bu beş postulat geometrinin temelini oluşturur.

1. Postulat: Farklı iki noktadan yalnız bir doğru geçer.

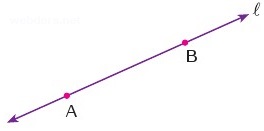
Yukarıda A ve B noktalarından l doğrusu geçer.

2. Postulat: Bir doğru parçası sınırsız bir şekilde uzatılabilir.

3. Postulat: Merkezi ve yarıçapı verilen bir çember çizilebilir.

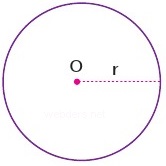
Merkezi O noktası ve yarıçapı r olan çember

4. Postulat: Bütün dik açılar eşittir.

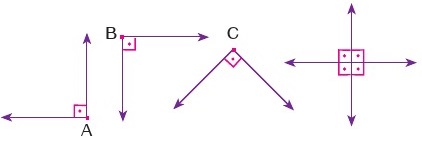
5. Postulat: Bir doğruya dışındaki bir noktadan yalnız bir pa­ralel doğru çizilebilir.

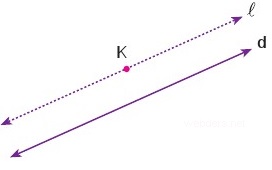
d doğrusuna paralel ve K noktasından geçen tek doğru l doğrusudur.

5. Postulat birçok matematikçi tarafından ilk 4 postula­tın bir sonucu olup olmadığı yönünde sorgulanmış ve bu sorgulamalar sonucunda postulat değiştirilerek, başka geometri sistemlerini ortaya çıkarmıştır.

Lobaçevski Geometrisi, Riemann Geometrisi gibi birçok geometri vardır. Günümüzde ise 50 den fazla geometriden bahse­dildiğini görebiliriz.

• Aksiyomlar kolay anlaşılır önermelerdir.
• Aksiyomlar arasında bir bağ yoktur, biri diğerinden elde edilemez.
• Aksiyomlar birbirleri ile uyum içindedir.
• Aksiyomlardan iki ya da daha fazlası kullanılarak bir önerme oluşturulursa bu önermeye teorem denir.

Aşağıda sık kullanılan bazı postulat örnek­leri verilmiştir, inceleyiniz.

Bir [AB] doğru parçası ve bir [XZ ışını verilsin.

|AB| = |XY| olacak şekilde [XZ ışını üzerinde sa­dece bir tane Y noktası vardır.

Bir çemberin çapı çemberi iki yarım çembere böler.

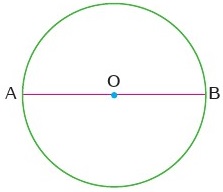
Her doğru parçasının yalnız bir orta noktası vardır.

Her açının yalnız bir açıortayı vardır.

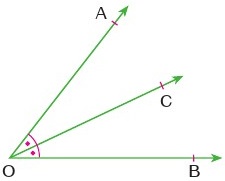
Düzlemde bir doğru ve bir nokta verilsin, bu noktanın üzerinde bulunduğu doğruya dik olan yalnız bir doğru vardır.

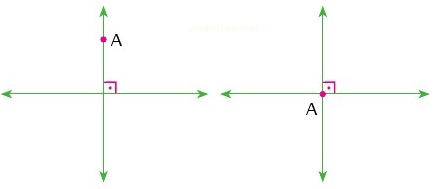
İki üçgenin kenarlarının uzunlukları birbirine eşitse bu üçgenler eştir.

Euclid (Öklid) (M.Ö. 325 - 265)

Egeli matematikçi Öklid'in kişisel yaşamı, aile çevre­si, matematik dışı uğraş veya meraklarına ilişkin hemen hiçbir şey bilin­memektedir. Bilinen tek şey; İskenderiye Kra­liyet Enstitüsü'nde dö­nemin en saygın öğret­meni; alanında yüzyıllar boyu eşsiz kalan bir ders kitabının yazarı olmasıdır.

Eğitimini Atina'da Platon'un ünlü akademisinde tamamladığı sanılmaktadır. O akademi ki giriş kapı­sında, "Geometriyi bilmeyen hiç kimse bu kapıdan içeri alınmaz!" levhası asılıydı. Öklid çağlar boyu yal­nız matematik dünyasının değil, matematikle yakından ilgilenen hemen herkesin gözünde özenilen, yetkin bir örnekti. Öklid, M.Ö. 300 sıralarında yazdığı 13 ciltlik yapıtıyla ünlüdür. Bu yapıt, geometriyi (dolayısıyla matematiği) ispat bağlamında aksiyomatik bir dizge olarak işleyen, ilk kapsamlı çalışmadır. 19. yüzyıl son­larına gelinceye kadar alanında tek ders kitabı olarak akademik çevrelerde okunan, okutulan Elementlerin, kimi yetersizliklerine karşın, değerini bugün de sürdür­düğü söylenebilir.

Öklid haklı olarak "geometrinin babası" diye bi­linir; ama geometri onunla başlamış değildir. Tarihçi Herodotus (M.Ö. 500) geometrinin başlangıcını, Nil vadisinde yıllık su taşmalarından sonra arazi sınırları­nı belirlemekle görevli kadastrocuların çalışmalarında bulmuştu. Geometri "yer" ve "ölçme" anlamına gelen "geo" ve "metrein" sözcüklerinden oluşan bir terimdir.

Kaleme aldığı Elementler, kendisini öncele- yen Thaies, Pythagoras, Eudoxus gibi, bilgin matematikçilerin çalışmaları üstüne kurulmuştu. Geo­metri bir önermeler koleksiyonu olmaktan çıkmış, sıkı mantıksal çıkarım ve bağıntılara dayanan bir dizgeye dönüşmüştü.

Öklid oluşturduğu dizgede birtakım tanımların yanı sıra, beşi "aksiyom" dediği genel ilkeden, beşi de "pos­tulat" dediği geometriye özgü ilkeden oluşan, on öncüle yer vermiştir (Öncüller, teoremlerin tersine ispatlanmaksızın doğru sayılan önermelerdir). Dizge tüm yetkin görünümüne karşın, aslında çeşitli yönlerden birtakım yetersizlikler içermekteydi.

Elementler'e bugüne değin yazılmış en büyük ki­tap gözüyle bakılsa yeridir. Bu kitap gerçekten Grek zekasının en yetkin anıtlarından biridir. Kitabın Greklere özgü kimi yetersizlikleri yok değildir, kuşkusuz: Dayandığı yöntem salt dedüktif niteliktedir; üstelik öncüllerini oluşturan varsayımları yoklama olanağı yoktur.

Omer Hayyam (1048 - 1131)

Hayyam takma adını, atalarının çadırcılık yapmaları yüzünden aldığı söylenir. Ömer Hayyam, za­manında daha çok, bilgin olarak ün kazandı.

Elde bulunan eserle­rinden, hayatıyla ilgili olayla­rı anlatan bazı kitaplardan, mantık, felsefe, matematik ve astronomi konularında çalıştığı, bu alanlarda düzenli bir öğrenim gördüğü anlaşılmaktadır.

Hayyam’ın fizik, metafizik, matematik, astronomi ve şiir konularında değişik eserleri vardır.

Nasuriddin Tusi (1201 - 1274)

O zamana kadar bu ilim dalı astronominin bir dalı olarak görülmekteydi.

Şubat 1201'de Horasan'ın Tus şehrinde doğdu. Hem din bilimleri hem de fen bilimleri dallarında eğitim gördü. Matematik, loga­ritma, mantık, hikmet ve idrak nazariyeleri ders­lerini okudu. Tusî'nin yaptığı ilmi faaliyetler­den önemli bir tanesi, trigonometriyi ayrı bir ilim dalı haline getirmesidir.

Ayrıca, bu ilim dalıyla ilgili eser de yazdı. Geomet­ride önemli bir otorite haline geldi ve kendisinden sonra gelen bilim adamları, ileri sürmüş bulunduğu tezlerin üzerine herhangi bir ilâve yapamadılar.

Geometride İspat

Geometride ispat bütün dallarda olduğu gibi çok önemlidir. Teorem ispatlanmadıkça geçerli sayılamaz. Geometride her şeyi ispatıyla bilmek bize çok avantaj sağlar. Geometride ispat yapabilmek için ispat yöntemlerini bilmemiz gerekir. İspat yöntemleri ve ispat biçimleri iki farklı kavramdır.

İki Kolonlu İspat

Bir önermenin ya da teoremin ispatı yapılırken ifa­deler birinci kolona, gerekçeler de ikinci kolona yazılır.

Bu ispat türünde elde olan veriler değerlendirilir. Her verilen ifadenin karşısına bilinen gerçekler yazılır. Böylece eksik parça tamamlanarak ispata gidilir.

İki kolonlu ispatta ispat iki kolonlu olacak şekilde karşılıklı tablo doldurularak yapılır.

Akış Diyagramlı İspat

Yazılan açıklamalardan adımlanarak ilerlenen ispat biçimidir. Verilen her veri bir sonraki adım için bir basamak oluşturur. Böylece sonuca gidilir.

Örnek verelim. Bir tam açı 360 derecedir teoremini ispatlarken en basit şekilde şöyle düşünebiliriz.

Bir tam açı = 2 doğru açı → Bir doğru açı = 180 derece → Bir tam açı = 2.180 = 360 derece olur.

Bu örnek akış diyagramlı ispatın belki de en basit örneklerinden biridir. Örnekteki basamaklar ve teoremin karmaşıklığı arttıkça diyagram içindeki koşul ve ok miktarı da artacaktır.

Paragraf İspat Biçimi

İspat detaylı açıkla ile yapılır. İspatı yaparken düz metin kullanılır. Paragraf şeklinde yazılan yazıyla ispatın maddeleri detaylı bir şekilde anlatılır.

Geometride bizim en çok kullandığımız tür paragraf ispat biçimidir. Bu sistemde eldeki veriler değerlendirilir. İşlem yapılır ve sonuca gidilir.

Geometride verilen teoremleri kullandığımızda ya da bu teoremleri elde ederken işlemler yaparız. Bu işlemlerde eşitliklerden yararlanırız. Eşitlikleri bazen ters işaretle çarparak işaret değiştirmesi yaparız. İşte bütün bunlar aynı zamanda paragraf ispat biçiminin birer alt parçasıdır.